Дэвид Уилкок - Исследования поля источника

В ноябре 2010 года Принц Чарльз выпустил новую книгу Гармония: Новый взгляд на наш мир . В ней он пользуется крупным научным исследованием Мартино, чтобы утверждать, что Вселенная является свидетельством проявления “грамматики гармонии”.

“Я был очарован, когда наткнулся на работу молодого геометра Джона Мартино, который учился в моей школе традиционного искусства несколько лет назад. Он провел тщательное изучение того, как орбиты планет относятся друг к другу и как модели, которые можно извлечь из этого, соответствуют вещам, созданным на Земле. Он нашел много красивых отношений… Все это служит замечательным свидетельством того, что во всем творении обнаруживается загадочное единство в паттернах. От самых мельчайших молекул до самых больших планетарных “частиц”, вращающихся вокруг Солнца, чтобы быть устойчивым, все зависит от невероятно простого, очень элегантного геометрического структурирования — грамматики гармонии”. [703] “Prince Charles Explores ‘Mysterious Unity’ of the Universe in New Book.” The Huffington Post . November 24, 2010. http://www.huffingtonpost.com/2010/11/24/prince-charles-harmony_n_786565.html

Точка зрения Кеплера на планеты впервые обсуждается на странице 12 книги Мартино.

“В поисках геометрического или музыкального решения орбит Кеплер заметил, что шесть гелиоцентрических планет означают пять интервалов. Тогда он попытался воспользоваться известным геометрическим решением — разместить между этими сферами пять Платоновых Тел”. [704] Martineau, John. A Little Book of Coincidence . Сочинение цитированное, стр. 2

На странице 14 все становится намного интереснее: “В частности… Кеплер заметил, что отношения между предельными угловыми скоростями планет представляют собой гармоничные интервалы”. Затем Мартино начинает оправдывать надежды.

“Два вписанных пятиугольника определяют положение орбиты Меркурия (99,4 %), пустое пространство между Меркурием и Венерой (99,2 %), соотношение орбит Земли и Марса (99,7 %) и пространство между Марсом и Церерой (99,8 %). Три вписанных пятиугольника определяют пространство между Венерой и Марсом (99,6 %) или средние орбиты Цереры и Юпитера (99,6 %). Скрытый паттерн?” [705] Там же, стр. 14

Безусловно, да. Пятиугольник обнаруживается и у додекаэдра с его пятиугольными гранями, и у икосаэдра с группами по пять треугольников, имеющих общие вершины. Поэтому мы успешно продвигаемся вперед.

На странице 20 Мартино высказывает интригующее предположение: хотя орбиты планет эллиптические, мы все же можем изучать основные пропорции, удерживающие их на месте, как будто орбиты сферические. Такой подход возможен потому, что естественно сферические энергетические поля сжимаются давлением и моментом движения через облака газа и пыли в галактике.

Я был потрясен, увидев следующее. Если вы нарисуете одну окружность для средней орбиты Меркурия, а затем соедините три подобные окружности для образования треугольника, а затем впишете все три окружности в еще одну окружность, вы получите орбиту Венеры (с точностью до 99,9 %). Конечно, поскольку окружности — это, на самом деле, сферы, получается вовсе не треугольник, это наш классический трехгранный тетраэдр — самое простое из всех Платоновых Твердых Тел.

Затем на странице 24 Мартино приводит замечательную геометрическую схему взаимосвязи между Землей, Венерой и Солнцем. Каждые восемь земных лет или тринадцать венерианских лет они входят в соединение для образования следующего угла совершенного пятиугольника, с 99,9 % точностью. И еще лучше: если мы работаем с самыми близкими и самыми удаленными точками, которых достигает Венера на протяжении восьмилетнего танца, образуется еще один еще больший пятиугольник, и вновь в совершенной пропорции к другим. Возможно, это результат Платоновых геометрий внутри сфер энергии, которые структурируются именно там, где проходят планеты. И вновь, в данном случае, благодаря додекаэдру и икосаэдру с их пятигранной симметрией.

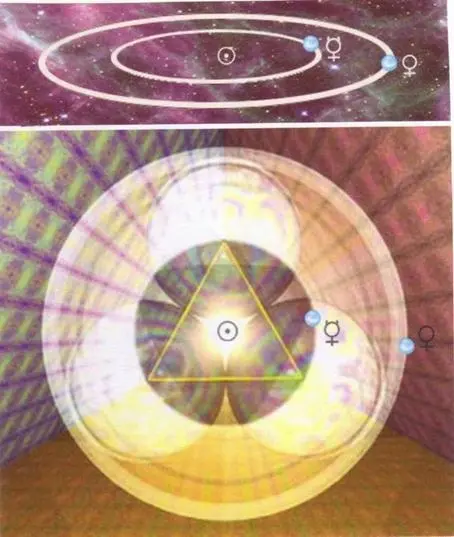
Джон Мартино иллюстрирует совершенное треугольное соотношение между орбитами Меркурия и Венеры. В трех измерениях треугольник становится тетраэдром.

На странице 32, благодаря работе Робина Хиза, мы находим геометрически точное соотношение между Землей и Луной. В году 12–13 полнолуний. Если мы нарисуем окружность (вновь, сферу) с диаметром в тринадцать единиц и впишем в нее совершенную пятиконечную звезду, тогда каждое ответвление звезды будет составлять 12,364 единицы. Это и есть истинное число полнолуний в год, в пределах уровня точности 99,95 %. И вновь, это позволяет предположить, что Землю и Луну связывает сфера силы, в которой движения Луны точно регулируются вращающимися вихревыми потоками гравитации внутри геометрии додекаэдра, целиком и полностью базирующиеся на пятимерной симметрии.