Хелен Девитт - Some Trick - Thirteen Stories

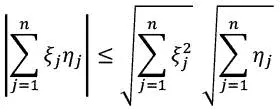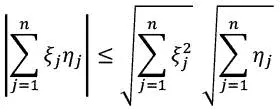
it holds for any pair of vectors x = (ξ 1… ξ n), y= (η 1… η n), or what is the same thing, for any two systems of real numbers ξ 1, ξ 2… ξ nand η 1, η 2… η n(this inequality was discovered by Cauchy in 1821).

The frame is very simple: x’s checked flannel shirt, with an open neck and short sleeve, has a Wittgensteinian innocence. The dark blue trousers are just trousers. The arm is long and bony. I am looking at the score of the music of the spheres. I gaze at this silent material for some time. The harmonies I see represented remain perfectly inaudible to me, but I see from the repose and concentration of x that x can hear them.

I have mastered subjects and failed to love them. I have looked at the sun and not been blinded; I have dimmed the sun. I will be a lover of the moon.

I lie on a bed with x. It is covered with a spread of purple chenille. The room is filled with humble objects lent dignity by the light of the moon: an electric kettle which does not switch off automatically; a mug with a picture of Miss Piggy; a box of Brooke PG Tips, a jar of coffee powder; a packet of My Mum’s digestives; a skimpy blue and red striped towel thrown over a chair; a shiny orange anorak.

On the desk are a pad of graph paper, four or five medium point blue Bic biros, two or three stubby pencils, a calculator. Ranged along the back against the wall are books: Diophantine Inequalities , I read on a spine. Bauer Trees of Sporadic Groups . Amenable Banach Algebras . Singular Perturbation Theory . I suppose that these books map out truth, or at any rate truths. I believe that mathematical truths are eternal, or rather timeless; but it is comforting rather than not to have so many of these truths allied to names and dates. I have not forgotten that the Cauchy-Bunyakovsky inequality was discovered by Cauchy in 1821! x has thrown a few library books on a chair by the door: Volterra Integrodifferential Equations in Banach Spaces and Applications . The Penrose Transform . Classical Fourier Transforms, Automorphic Forms, Shimura Varieties, and L-functions . These names commemorate persons who heard, wrote down snatches of the piece. I am happy for them. At the same time it is sheer accident that one rather than another happened to do so — x sometimes tells me stories of simultaneous discovery. x can’t see why these delight me. Sometimes I ask x ‘Who was Banach?’ ‘What about Shimura?’ ‘Just who was Penrose, anyway?’ just for the pleasure of hearing x’s confessions of ignorance, or professions of knowledge — the answer, when x has one, is always of the form ‘A was someone who discovered that B.’

X, who had views on everything, would not have stood for it. What was his line? ‘The truth is that counting has proved to pay.’ ‘It can’t be said of the series of natural numbers that it is true, but: that it is usable, and, above all, it is used.’ This sounds familiar — I’m sure I remember X quoting it — but whether pro or con I can’t recall. Certainly mathematics were not to have the privilege of referential semantics, but the ins and outs of the arguments for levelling escape me now. I look at the face of x, calmly intent upon a book: the light must come from somewhere.

x sometimes has a book propped open against a knee. I look over x’s shoulder at Probability Approximations via the Poisson Clumping Heuristic ; my eyes wander restfully across a page of Greek letters and brackets. x holds, sometimes, a small spiral pad, one of the blue Bic biros, from time to time x scrawls a note, pursues a line of thought in strings of symbols which modulate down the page. x’s wrist lies along the edge of the pad. I see the articulation of the joint, thin delicate bones jut out beneath thin pale freckled skin; x’s large knuckles clamp round the pen, bitten fingers press into the palm. How close they look! I am seeing the moon through a telescope. It is not the smooth flat surface you imagine, seeing that disc suspended in the sky; but there is a kind of wonder in seeing the rocky cratered plain which nevertheless disperses light — in seeing how, even at closer range, the line between black and brilliant white is absolute.

I put my arm around x. x’s forehead is very high and pale, the skin stretched tight over the sleek pure curve of the skull. I lay my forehead against it and close my eyes. I do not strain my ears to pierce the silence; I know that within that bone and blood, a few centimetres away, plays the music of the spheres.

He was a pianist. He was born on the island of Shikoku, where his father had some kind of post in the administration of the prefecture of Tokushima. His mother was from Tokyo. When she married his father she had her piano brought down on the ferry to her new home. He was taught from the age of two by his mother, and from the age of eight by a woman who had studied in Paris with Koslowski until the mid-40s, when she had cut short a promising career to keep house for her widowed father.

Koslowski had said

Of all my pupils the one who showed the finest sensibility in the interpretation of Chopin was Mlle Matsumoto. To praise her technique is to say nothing. The simplicity and ease with which she executed even the most difficult passages, the absence of any kind of affectation or showmanship in pieces where it is too common to see talent on display, while the pianist plays the virtuoso, all this gave one some notion of the style of performance favored by the composer himself. We know for example on the authority of de Bertha that Chopin obtained his effects by methods very different from those of today, relying not on brute force but on gradations achieved through an infinite extension of the piano . This was to have the nuances, the expressive shading of the human voice or of that instrument which comes closest to the voice, the violin. His masters were a Paganini, a Bellini, a Catalani. What was remarkable was Mlle Matsumoto’s ability to realize the impossible, to transform a percussive instrument into one which had the fluidity of the voice.

Her retirement has robbed music of a precious ornament but it is impossible to regret it, for it springs from the very thing which made her playing incomparable — I refer to the complete absence of self…

This was not the opinion of the pupil of Koslowski’s who achieved the greatest renown. He did not hesitate to express his views on the Automaton in the most intemperate language.

Morhange said later

All sorts of contemptible things were done during the War and even later, and they did not stop at the door of the Conservatoire. One of these was old Koslowski’s retention of Mlle Matsumoto, undoubtedly to curry favor with the Nazis, while at the same time washing his hands of anyone with any sort of Jewish connection —

Elle avait du talent, oui, mais elle jouait d’une façon tout à fait machinale, there was a tiresome perfection about her performance —

Koslowski said later that he had been obliged to cut back on his teaching and that M. Morhange had always shown himself so absolutely indifferent, if not positively hostile, to all suggestions on his own part that he had not supposed it would be a hardship to the young man to be deprived of them.

Morhange said that after the War it was of course even more necessary for him to present his actions under the guise of a simple pedagogical decision, one could naturally not admit that anyone had been excluded on account of the Semitic factor, it was therefore necessary to insist on the lack of talent, on aesthetic defects, which by coincidence happened to be found in Jewish persons.