Марк Хэддон - Загадковий нічний інцидент із собакою

Коли він розказав про це пані, яка сиділа нагорі на касі, то йому сказали, що це був Тук, привид монаха-францисканця, який колись жив у монастирі, що стояв на цьому місці сотні років тому, і саме тому торговий центр називався «Торговий центр Сірого Монаха», і вони вже до нього звикли й зовсім не боялися.

Зрештою вчені відкриють щось таке, що пояснить існування привидів, так само як вони відкрили електрику, що пояснило природу блискавки, і це може бути пов’язано з роботою людського мозку або з чимось в електромагнітному полі землі, або це взагалі буде якась нова сила. І тоді привиди вже не будуть загадкою. Вони стануть такими самими, як електрика, веселки та сковорідки з антипригарним покриттям.

Але інколи загадка зовсім не є загадкою. Ось приклад загадки, яка насправді нею не є.

У нашій школі є ставок із жабами, які там живуть, щоби ми вчилися ставитися до тварин з добротою й повагою, оскільки деякі діти зі школи огидно поводяться з тваринами й гадають, що давити хробаків або кидати в котів каміння — це кумедно.

Інколи випадають роки, коли в ставку багато жаб, а інколи випадають роки, коли мало. І якщо намалювати графік кількості жаб у ставку, то він мав би такий вигляд (але цей графік, що називається, гіпотетичний, а це означає, що цифри не відповідають дійсності і вони надані для прикладу):

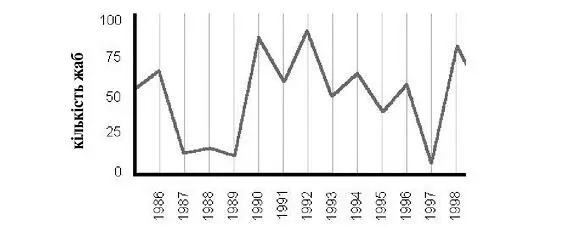
І якщо подивитися на цей графік, то можна вирішити, що 1987 року була дуже холодна зима, як і 1988-го, 1989-го та 1997-го років, або що прилітала чапля й з’їла багато жаб (інколи чапля насправді прилітає й намагається з’їсти жаб, але їй заважає сітка, яку натягнули над ставком).

Але інколи холодні зими, коти чи чаплі бувають ні до чого. Інколи справа тільки в математиці.

Ось формула для обрахунку певної популяції тварин:

Nнова = λ(Nстара)(1 – Nстара)

У цій формулі щільність населення позначена як N. Коли N = 1, то популяція досягає найбільшої кількості. А коли N = 0, то популяція зникає. Nнова — це популяція певного року, а Nстара — це популяція попереднього року. А λ є тим, що називається константою.

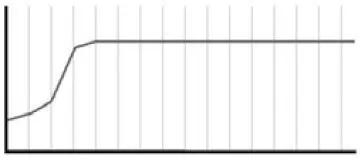
Коли λ менше від 1, то популяція зменшується й зменшується, поки не зникає. А коли λ між 1 і 3, то популяція зростає й залишається стабільною, ось так (усі ці графіки також гіпотетичні):

А коли λ між 3 й 3,57, то популяція стає циклічною, ось так:

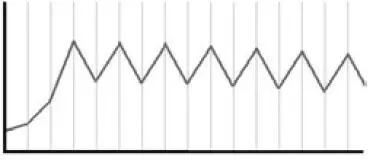
Але коли λ більше від 3,57, то популяція стає хаотичною, як на першому графіку.

Це було відкрито Робертом Мейєм, Джорджем Остером і Джимом Йорком. І це означає, що інколи речі стають такими складними, що неможливо передбачити, що відбудеться в майбутньому, але всі вони підкоряються дуже простим законам.

А це означає, що інколи популяція жаб, хробаків або людей може вимерти без будь-якої на те причини, просто тому, що так працюють числа.

Минуло шість днів, перш ніж я зміг повернутися в кімнату Батька, щоби зазирнути в коробку для сорочок у шафі.

Першого дня — а це була середа — Джозеф Флемінг зняв штани й сходив у туалет у роздягальні, і його калі були по всій підлозі, а потім він почав їх їсти, але містер Девіс його зупинив.

Джозеф їсть усе вряд. Якось він з’їв один із тих маленьких синіх блоків із дезінфектором, що висять в унітазах. А іншого разу з’їв банкноту в £50 із гаманця своєї матері. Він їсть нитки, гумки, носовички, писальний папір, фарби й пластикові виделки. Також він б’ється підборіддям і багато кричить.

Тайрон сказав, що в калях були кінь і свиня, а я заперечив, що це дурниці, але Шивон підтвердила, що він правий. То були маленькі пластикові звірі з бібліотеки, яких вчителі використовують, коли розповідають якісь історії. І Джозеф їх з’їв.

Тож я заявив, що не ходитиму в туалет за переодягальнею, оскільки на підлозі були калі і мені незатишно про це думати, хоча містер Еннісон вже встиг прийти й прибрати їх. Я напісяв у штани, і довелося вдягати змінну пару з шафи для змінного одягу в кабінеті місіс Ґасконь. Шивон сказала, що протягом двох днів я можу ходити в туалет учителів, але лише протягом двох днів, а потім мені знову доведеться користуватися учнівським туалетом. І на цьому ми домовилися.

Другого, третього й четвертого дня — а то були четвер, п’ятниця й субота — нічого цікавого не відбулося.