Шон Кэрролл - Вечность. В поисках окончательной теории времени

a x = a · a · a · a · a · a … a · x раз.

К сожалению, это определение может создавать впечатление, что показательная функция имеет смысл только в том случае, если степень x – это положительное целое число. Как умножить число на само себя минус два раза? Или 3,7 раза? Здесь вам остается только верить, что магия математики позволяет определять показательную функцию для любого значения x . Результатом является гладкая функция с очень маленьким значением, когда x – отрицательное число, но резко возрастающая, когда x становится положительным, как показано на рис. П1.

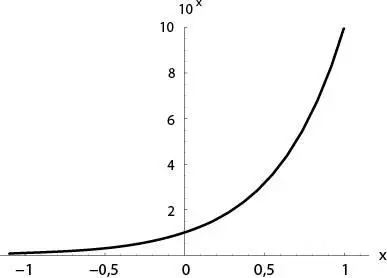
Рис. П1.Показательная функция 10 x. Обратите внимание, что она возрастает так быстро, что совершенно невозможно изобразить ее для больших значений x

Что касается показательных функций, есть две важные вещи, о которых необходимо помнить. Любое основание, возведенное в степень 0, равно 1, а любое основание, возведенное в степень 1, равно самому себе. Для основания 10 это выглядит так:

10 0= 1,

10 1= 10.

Если степень – это отрицательное число, то результатом операции является число, обратное результату возведения в соответствующую положительную степень:

10 –1= 1/10 1= 0,1,

10 –3= 1/10 3= 0,001.

То, что вы видите выше, – это всего лишь конкретные примеры из более общих свойств, которым подчиняется показательная функция. Одно из этих свойств является невероятно важным: если умножить два числа, представляющих собой одно и то же основание, возведенное в разные степени, то при перемножении степени складываются, а основание остается тем же самым:

10 x· 10 y= 10 (x+y).

То же верно и в обратную сторону: показательная функция от суммы степеней равна произведению двух чисел, равных основанию, возведенному в эти степени. [311]

Большие числа

Нетрудно понять, почему показательная функция так полезна: числа, с которыми нам приходится иметь дело, иногда бывают чрезвычайно большими, а с помощью возведения в степень вы можете превратить число средней величины в просто огромное. Как мы обсуждали в главе 13, количество различных состояний, необходимых для описания возможных конфигураций нашего сопутствующего объема Вселенной, равно примерно

10 10120

Это число настолько неимоверно, невообразимо огромное, что было бы совершенно непонятно, с какой стороны вообще подступиться к его описанию, если бы на помощь не пришло возведение в степень.

Давайте рассмотрим несколько других больших чисел, для того чтобы оценить, насколько огромно это. Один миллиард равен 10 9, тогда как один триллион – это 10 12; с этими значениями мы хорошо знакомы благодаря обсуждениям экономики и правительственных трат. Количество частиц в нашей наблюдаемой Вселенной составляет около 10 88; настолько же велика была энтропия в ранние времена. Теперь, когда у нас есть черные дыры, энтропия наблюдаемой Вселенной равна приблизительно 10 101, хотя вполне могла бы дорасти до 10 120. (Это число, 10 120, также представляет собой отношение предсказываемого значения плотности энергии вакуума к наблюдаемой плотности.)

Для сравнения, энтропия макроскопического объекта, такого как чашка кофе, – где-то 10 25. Это значение сравнимо с числом Авогадро, которое равно 6,02 · 10 23– примерно столько атомов составляют один грамм водорода. Число песчинок на всех пляжах Земли – приблизительно 10 20. Число звезд в типичной галактике – около 10 11, а число галактик в наблюдаемой Вселенной – около 10 11, то есть в наблюдаемой Вселенной существует примерно 10 22звезд – немного больше, чем песчинок на Земле.

Базовые единицы измерения, используемые физиками, – это единицы времени, длины и массы; используются также их комбинации. Самый короткий интервал времени, представляющий интерес, – это планковское время, примерно 10 –43секунд. Предположительно инфляция продолжалась около 10 –30секунд или меньше, хотя это значение чрезвычайно неточно. Вселенная создала гелий из протонов и нейтронов где-то через 100 секунд после Большого взрыва, а прозрачной стала в момент рекомбинации, 380 000 лет (10 13секунд) спустя. (В одном году около 3 · 10 7секунды.) Сейчас наблюдаемой Вселенной 14 миллиардов лет (примерно 4 · 10 17секунды). Еще через 10 100лет или около того все черные дыры практически полностью испарятся, оставив после себя холодную и пустую Вселенную.

Самая маленькая длина – это планковская длина, около 10 –33сантиметров. Размер протона – примерно 10 –13сантиметров, а размер человеческого существа – примерно 10 2сантиметров (это очень низкое человеческое существо, но мы сейчас оперируем приблизительными значениями). Расстояние от Земли до Солнца – около 10 13сантиметров; расстояние до ближайшей звезды – около 10 18сантиметров, а размер наблюдаемой Вселенной – около 10 28сантиметров.