Л. Наумова - Основы общей экологии

Модель экспоненциального роста описывается J-образной кривой: в условиях постоянного поступления ресурсов скорость роста популяции увеличивается и кривая взмывает вверх (рис. 15). Модель может быть описана уравнением:

N t= N 0е rt,

в котором N t– численность популяции через очередной промежуток времени (t),

N 0– исходная численность,

е – основание натурального логарифма,

r – коэффициент размножения (репродуктивный потенциал, разность относительной рождаемости и относительной смертности, т.е. число родившихся или умерших особей отнесенное к числу особей популяции в начале промежутка времени t).

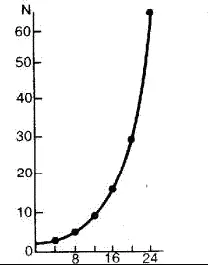
Рис. 15. Экспоненциальная модель роста численности популяции одноклеточного организма, делящегося каждые 4 часа.

Чтобы рост популяции соответствовал этой модели, величина коэффициента r должен быть постоянной, т.е. должно быть постоянным среднее количество потомков на одну особь (если r = 0, т.е. рождаемость равна смертности, то численность популяции не растет).

В зависимости от величины r увеличение численности особей может быть быстрым и достаточно медленным. Ч. Дарвин рассчитал потенциальные возможности роста популяций разных организмов при реализации экспоненциальной модели. По его оценкам, число потомков одной пары слонов – животных, размножающихся чрезвычайно медленно, – через 750 лет достигнет 19 млн. Если же обратиться к организмам, живущим не так долго и размножающимся более быстро, то цифры будут еще более впечатляющими. У бактерий, которые делятся каждые 20 минут, из одной бактериальной клетки через 36 часов может образоваться биомасса, которая покроет весь земной шар слоем толщиной 30 см, а еще через 2 часа – слоем в 2 м.

«Поскольку ни бактерии, ни слоны не покрывают землю сплошным слоем, очевидно, что на самом деле в природе экспоненциальный рост популяций организмов или не происходит вообще, или же происходит, но в течение непродолжительного времени, сменяясь затем спадом численности или выходом ее на стационарный уровень» (Гиляров, 1990, с. 77).

В природе экспоненциальный рост численности популяций наблюдается в сравнительно кратковременные периоды их жизни при особо благоприятных условиях, когда постоянно пополняются ресурсы. Так в озерах умеренных широт весной после таяния льда в приповерхностном слое воды содержится много биогенных элементов. По этой причине после прогревания воды здесь наблюдается быстрый рост численности диатомовых и зеленых водорослей. Однако он также быстро прекращается, когда эти ресурсы оказываются израсходоваными и, кроме того, зоопланктон начнет активно выедать водоросли (т.е. за счет регулирования плотности популяций «снизу» и «сверху»).

Пример экспоненциального роста популяции – история интродукции северного оленя на острова. Так от 25 особей (4 самца и 21 самка), завезенных в 1911 г. на остров Святого Павла (Берингово море), к 1938 г. сформировалась популяция из 2000 оленей. Однако затем последовал спад численности, и к 1950 г. сохранилось всего 8 особей. Причина краха популяции – нарушение отношений «растение – фитофаг» (см. 8.3) ввиду отсутствия в пищевой цепи третьего звена – хищника.

Логистическая модель роста популяций, описываемая S-образной кривой (медленный рост – быстрый рост – медленный рост, рис. 16), была предложена также в начале 19-го столетия бельгийским математиком П.-Ф. Ферхюльстом, а затем уже в 20-е гг. нашего столетия переоткрыта американскими учеными Р. Перлем и Л. Ридом. П.В. Турчин считает эту модель отражением закона «самоограничения роста любой популяции».

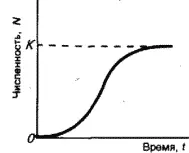
Рис. 16. Логистическая модель роста популяции. К – предельная численность

Причины замедления роста популяции могут быть самыми различными: выедание ресурсов, влияние эффекта скученности (у грызунов при этом снижается интенсивность репродуктивного процесса), отравление местообитания прижизненными выделениями, выедание популяции хищниками и т.д.

Тем не менее и эта кривая является идеализацией, так как крайне редко проявляется в природе. Очень часто после того, как рост популяции выйдет на плато (достигнет предела К, соответствующего количеству ресурсов), происходит внезапное уменьшение ее численности, а потом популяция вновь быстро растет. Таким образом, ее динамика оказывается состоящей из повторяющихся логистических циклов.