Once back in Princeton, we would notice that our trunk key had disappeared. Kurt immediately wrote Mrs. Frederick to accuse her of stealing it. What a charming impression we must have left behind!
We followed Parker Point Road, a narrow lane along the shore. Through a screen of pines, we could see magnificent Blue Hill Bay, dotted with islands. Then we took a path toward an attractive cove that we had found on an earlier walk. I spread a quilted coverlet over the rocks. Kurt valued his comfort.
“It’s too damp to stop here.”
“We’re at the seashore, Kurt! In town you’re always complaining of how stuffy it is.”
He sat down unwillingly.
“We could have lunch outdoors today. I’d like to try clam soup.”
Three boats were moored close to shore and their halyards slapped gently against the masts to the rhythm of the waves. Gulls chased each other, skimming over the foam. In the distance, I could see a lumbering shape haul itself onto a rocky ledge. The sun warmed my shoulders. I breathed the air deeply, dazzled by the quiet splendor. The war was so far away.
“I could look at this forever.”
“You don’t know how to swim, Adele. You should learn.”
Although the day was warm, he had bundled himself up in his overcoat.
“Do you see that amazing blue where the sea and the sky meet?”
The brim of his hat rose barely a fraction.
“You’re not even looking! What do you think about when you’re in front of the ocean?”
“I see a field of wave interactions whose complexity fascinates me.”
“How sad! You should bathe your mind in all this beauty.”
“Mathematics has true beauty.” 6
His matter-of-factness cut against the spirit of the moment.
“What’s bothering you now? You don’t talk to me about your work anymore.”
If sarcasm had had any effect on him, I would have added, “You haven’t talked to me about anything for a long time.” I took his hand; it was cold and tense.
“I’m wondering about the existence of infinity.”
He let go of my hand and stood looking out at the sea. A small wave licked the toe of his shoe. He backed away, scowling.
“When you look at the ocean, you might have a sensation of infinity. Nonetheless you can’t measure this infinity or, rather, you can’t understand it.”
“You might as well try to empty the sea with a teaspoon!”
“We have made teaspoons, as you put it, to define infinity, but how can we know that these mathematical tools are not just an intellectual construct?”
“Infinity surely existed before man invented mathematics!”
“Do we invent mathematics, or do we discover it?”
“Does a thing exist only if we have the words to talk about it?”
“That’s a vast question for your small brain.”
I drew an ∞ over my heart.
“The infinities that occupy me at the moment relate to set theory. It’s very different.”
“What a cockamamy idea! Infinity is infinity, there’s nothing bigger.”
“Some infinities are greater than others.”
He carefully lined up three pebbles he had picked up from the beach.
“Here is a set. A pile, if you like. It makes no difference if they’re pebbles or pieces of candy, think of them as elements.”
I stood up to show that I was paying faithful attention. He rarely made an attempt to teach me anything.
“I can count them: one, two, three. So I have a set with three elements. I can then decide to make subpiles: the white with the gray, the white with the black, the black with the gray; then the white alone, the gray alone, the black alone; all three together; and none. I have eight possibilities, eight subsets. The set of the parts of a set always has more elements than the set itself.”
“So far, so good.”
“If you lived for several centuries, you could count all the pebbles on this beach. And in theory if you lived forever, you could spend the time counting, but … there is always a larger number.”
“There is always a larger number.”
I turned these words over in my mouth; they had a peculiar taste.
“Even if you could count to infinity, there would still always be a bigger infinity around the corner. The set of the parts of an infinite set is greater than the infinite set itself. Just as the possible permutations of these three pebbles is greater than three.”
“That’s a funny little game of construction!”
“For you to understand the next part, you have to be clear on the difference between cardinal and ordinal numbers. Cardinal numbers allow you to count the elements in a set: you’ve got three pebbles. Ordinals put the elements in order: here’s the first pebble, the second, and the third. The cardinal number counts the elements up to infinity without assigning an order to the elements. The symbol used for the cardinality of an infinite set is the Hebrew letter aleph.
He drew an esoteric sign in the sand, then wiped his finger with his handkerchief: 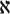 . I handed him a stick of driftwood, which he accepted with the ghost of a smile in place of thanks.
. I handed him a stick of driftwood, which he accepted with the ghost of a smile in place of thanks.
“The three pebbles stand for natural numbers, the numbers we all use to count normal objects: 1, 2, 3, etc. This set is called 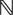 .”
.”
He drew an 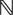 and made a big circle around it, putting the three pebbles inside.
and made a big circle around it, putting the three pebbles inside.
“Why? Are there others?”
I liked hearing him laugh. It happened so rarely.
“We have, among others, the integers: the set 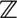 . The integers are defined with respect to zero. We add the minus sign to a whole number to show that it is below zero: -1 is less than zero; 1 is more than zero. Do you remember in the train, people were talking about a temperature of -50 degrees Celsius? To be more accurate, they should have said 50 degrees below what the Celsius scale determines as zero degrees of temperature.”
. The integers are defined with respect to zero. We add the minus sign to a whole number to show that it is below zero: -1 is less than zero; 1 is more than zero. Do you remember in the train, people were talking about a temperature of -50 degrees Celsius? To be more accurate, they should have said 50 degrees below what the Celsius scale determines as zero degrees of temperature.”
He drew a larger circle around the first, then a third around the other two. He labeled each with a large, elegant capital letter: 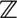 , then
, then  .
.
“  is the set of rational numbers, which includes all the whole-number fractions like 1/3 and 4/5.”
is the set of rational numbers, which includes all the whole-number fractions like 1/3 and 4/5.”
“N, Z, Q … My poor brain!”
“Common sense will tell you that the set of all natural numbers 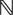 is smaller than the set of all integers
is smaller than the set of all integers 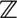 . The set 1, 2, 3 is smaller than the set 1, 2, 3, -1, -2, -3. In the same way, the set of all integers
. The set 1, 2, 3 is smaller than the set 1, 2, 3, -1, -2, -3. In the same way, the set of all integers 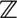 is smaller than the set of all rational numbers
is smaller than the set of all rational numbers  . The set 1, 2, 3, -1, -2, -3 is smaller than the set 1, 2, 3, -1, -2, -3, 1/2, 1/3, 2/3, -1/2, -1/3, -2/3, etc. All these sets are embedded one within the other. The natural numbers, you could say, form the smallest pile, and the rational numbers the largest.”
. The set 1, 2, 3, -1, -2, -3 is smaller than the set 1, 2, 3, -1, -2, -3, 1/2, 1/3, 2/3, -1/2, -1/3, -2/3, etc. All these sets are embedded one within the other. The natural numbers, you could say, form the smallest pile, and the rational numbers the largest.”
“Like cooking pots! So they have different infinities?”
“Wrong! They have the same cardinality. I’ll spare you the proof. Georg Cantor proved it with the help of a bijective function in the first case and using a diagonal argument in the second.”
Читать дальше

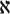 . I handed him a stick of driftwood, which he accepted with the ghost of a smile in place of thanks.
. I handed him a stick of driftwood, which he accepted with the ghost of a smile in place of thanks.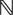 .”
.”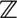 . The integers are defined with respect to zero. We add the minus sign to a whole number to show that it is below zero: -1 is less than zero; 1 is more than zero. Do you remember in the train, people were talking about a temperature of -50 degrees Celsius? To be more accurate, they should have said 50 degrees below what the Celsius scale determines as zero degrees of temperature.”
. The integers are defined with respect to zero. We add the minus sign to a whole number to show that it is below zero: -1 is less than zero; 1 is more than zero. Do you remember in the train, people were talking about a temperature of -50 degrees Celsius? To be more accurate, they should have said 50 degrees below what the Celsius scale determines as zero degrees of temperature.” .
.










