Neel Mukherjee - The Lives of Others

Swapan had been in similar situations over the last year and a half. Still, that childhood indoctrination in the moral principle of just deserts — that the right and the deserving always win at the end of the day — was a terribly tenacious thing, difficult to shake off.

‘Listen, don’t be stupid,’ Samiran had advised. ‘Which college is going to give you a lectureship? Are you a Party member? Even then, you’ll have to serve time in Siberia — in those appalling colleges in the sticks: Bardhaman, Kalyani, Jalpaiguri. . are you prepared for that fate worse than death?’

So St Lawrence it was, to stave off debts, rent and bills in arrears, the shrinking of days through squalor. Every day now, work on Riemann’s zeta function seemed more and more like the depleting memory of having had a dream, not even of the dream itself. His reality, instead, was a bunch of slothful, slow-witted, smelly idiots, not one of whom, not a single one of them, was destined for anything higher than a nine-to-five job as a low-to-middle ranking manager in a local bank. And that was the destiny of the best of the lot.

Well, maybe there was one exception, that eerily quiet and shy new arrival, Swarnendu Ghosh, whose sole aim in life, it would appear, was to make himself invisible. That boy, he knew, was gifted; not only full marks in mathematics in the few exams and class tests he had taken, but also something about the way he did mathematics had alerted him to this boy’s talent. It was not the standard cud-chewing ease with set questions and exercises that came with regular practice and drill, but something far deeper, something to do with an effortlessness of movement in the world of abstraction. The boy thought mathematically.

But he too seemed to be paying no attention that day, staring at a small collection of paper on his desk, so still that he appeared not even to be breathing. Right, time for some order.

‘Swarnendu,’ he called.

The boy remained shut in his world.

‘Swarnendu!’

No reply. No change in posture.

‘S-W-A-R-N-E-N-D-U!’ It was a bit mean to pick on him when dozens of others would have done — every one of them was inattentive — but something about the paradox of the boy’s seemingly endless drift, yet brutal concentration, caught his interest.

Now the class was focused on this diversionary drama, a welcome relief from the impenetrable talk of horizontal and vertical axes and anticlockwise movement of a circle and intersection with the positive horizontal axis. A tiny choir of tittering and whispering had erupted.

Swapan Adhikari stepped off his dais and strode over to Swarnendu.

‘What is keeping you from paying attention? Let’s see,’ he said and pulled the sheaf of paper away. The boy involuntarily tried to protect it by bringing down his arms, but too late; he had been taken by surprise.

‘Since you’re such a whizz at mathematics that you think there’s no need to listen to what I say in class, why don’t you tell us about the cosine curve? And stand up when I’m speaking to you.’

It was cruel, Swapan Adhikari thought, but he had the right to make them take notice. The boy stood up, his eyes fixed to the ground at his feet.

‘Go on, then, tell us something about the cos curve.’

Silence.

‘I see you’re not with us yet. Can you tell us the relationship between the sine and the cosine curves?’ That’ll teach him.

The boy looked up at the board, then down again.

‘Here, go up to the blackboard. Take this piece of chalk. I want you to explain to the class.’

He had pushed the boy too far; he looked as if he was going to burst into tears. Instead, he obliged. He stood facing the blackboard, his back to the class, and held this pose for a minute, two minutes, absolutely still. Then he started writing:

2π = 1 complete revolution of circle .

He drew the x and y axes afresh, showing all four quadrants, and marked off equal intervals on the x-axis: -2π, -1.5π, -π, -0.5π, 0, 0.5π, π, 1.5π, 2π. Then he plotted a sine curve on it, beginning at (0,0) and marked it, accurately, y = sinx. Even the sound of ordinary susurrus had been hushed in the classroom. Swapan Adhikari felt the beginnings of what he could only think of as an effervescence somewhere in his throat, trying to move up and out, as he watched from the side Swarnendu plotting a cosine curve, again with cast-iron accuracy, on the same axis and naming it y = cosx. He mumbled something. Swapan Adhikari asked him to repeat it.

Sona mumbled, ‘The cosine curve is to the left of the sine curve by a distance of .’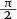

He wrote on the board again:

cosx = sin (x + 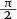) or sinx = cos (x — ).

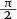He stopped for a bit, looked at his teacher for an instant, immediately looked down again, then once again faced the board. He wrote:

From the above, sin 2x + cos 2x = 1.

Again he glanced briefly at Mr Adhikari. This time he gathered up enough courage to ask, ‘Shall I prove it?’

Swapan Adhikari shook his head and said, ‘No. Go back to your seat now.’ He was going to add, redundantly, he felt, ‘Pay heed to what I’m teaching next time’, but decided not to.

The boy meekly returned to his bench, his expression of desired erasure unchanged; not an atom of triumphalism or self-satisfaction anywhere. But that was not what was going through Swapan Adhikari’s mind at all. What dazed him was the clarity of the boy’s mind, of his impeccable return to first principles and proceeding from there. This new pupil in Class Seven had just elucidated a topic that he was three years away from being taught in school.

At home he looked at the bundle of papers he had confiscated: a collection of different kinds, ruled, plain, of different sizes, quality and colour, all held together by a rusty safety pin. The first ten or twenty seconds of browsing was a blur of numbers and alphabets and faux-equations, and then it hit him with a force that could have lifted him clean off the ground if it had had a material correlate — the boy was trying to prove Fermat’s two-square theorem. First, over several sheets there was an ultimately successful attempt to prove that the set of all sums of two squares was closed under multiplication. Using that as a starting point, he had embarked on a proof of p = x 2+ y 2iff p ≡ 1 (mod 4). There were shortcuts the boy clearly did not know about, so he had spent a lot of time reinventing the wheel. Shorn of the circularities, the reiterated steps, the occasional cul-de-sacs, he had been engaged in working out from scratch Euler’s proof by infinite descent. The notations were unconventional, there was a lot of chasing of his own tail, but there it was: a messy proof, not parsimonious, not austere, but a proof nevertheless, one even assuming a knowledge of relatively prime and — miraculous, this — a feeling for the notion of finite difference.

On another page there were series of numbers, written one after the other, line after line. A few minutes’ contemplation of those revealed that the boy was trying to feel his way towards prime gaps and twin primes. On yet another, an innocently formulated: ‘if a > 1, then a. . P. . 2a?’; the boy did not know that he had stumbled upon Bertrand’s theorem. Swapan Adhikari had to prove it in his final exams for the BA (Hons) degree. 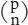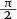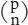There was a long-winded working-out of the binomial theorem — he must have had access to some kind of intermediate mathematics books to symbolise binomial coefficients correctly as and even a knowledge of combinatorials in his use of n! — and its correct proof using induction. Buried deep within was some incipient thinking about asymptotic equality leading on from logarithms and the prime counting function.