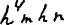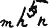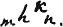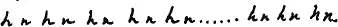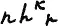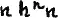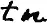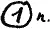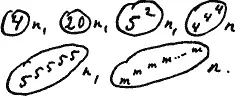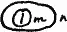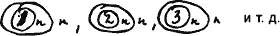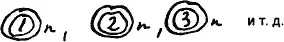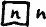Даниил Хармс - Неизданный Хармс

Мы можем это выражение записать проще, а именнотак:

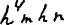
или ещё проще:

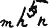
или общий случай

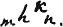
где k мы будем называть чином.

Рассмотрим случай титулования, где числа титулоых коэффициентов равны друг другу и равны кореному основанию:

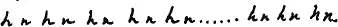
Если всех коэффициентов f, а f + 1 =k

гы мы это вырожение можем записать так:

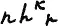
Если k = n, то

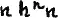
или просто:

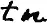
Это есть чинование n

Будем процесс титулования n изоброжать так:

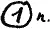
А процесс чинования n изображать так:

То легко себе представить процесс:

А так же:

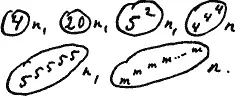
и наконец:

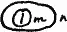
Возможны и такие случаи:

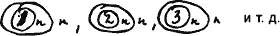
Изобразим это так

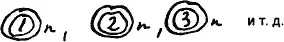
Возмём случай:

Легко представить как число колец будет рости. И когда достигнет n изобразим полученное выражение так:

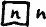
Число квадратов так же может достигнуть n. Изобразим это так:

И так можно продолжать без конца. Круг был у нас первой сменой фигур, квадрат-второй, трехугольник – третей и т. д. Но будем квадрат всегда считать n-ой сменой фигур.

Поэтому выражение:

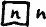
будет иметь определённое значение и мы будем называть:

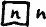
– поднятием числа n.

или поднятое n.

Для краткости можем вырожение

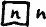
изображать просто так:

25 мая 1931 года.

♂ 2 августа 1932 года.

Курск.

«Безконечное, вот ответ на все вопросы. Все вопросы имеют один ответ. А потому нет многих вопросов, есть только один вопрос. Этот вопрос: что такое бесконечное?»

Я написал это на бумаге, перечитал и написал дальше:

«Безконечное, кажется нам, имеет направление, потомучто мы всё привыкли воспринемать графически. Большему соответствует длинный отрезок, а меньшему – короткий отрезок. Безконечное, это прямая, не имеющая конца ни в право, ни в лево. Нотакая прямая недоступна нашему пониманию. Если на идеально глатком полу, лежит глаткий, плоский предмет, то овладеть этим предметом мы можем только в том случае, если мы доберёмся до его краёв; тогда мы сможем поддеть рукой под край этого предмета и поднять его. Бесконечную прямую не подденешь, не охватишь нашей мыслею. Она нигде не пронзает нас, ибо для того чтобы пронзить что-либо, должен обнаружиться ее конец, которого нет. Это косательная к кругу нашей мысли. Ее прикосновение так не материально, так мало, что собственно нет никакого прикосновения. Оно выражается точкой. А точка, это бесконечно несуществующая фигура. Мы-же представляем себе точку, какбесконечно маленькую точечку. Но это ложная точечка. И наше представление о бесконечной прямой – ложное. Бесконечность двух направлений, к началу и к концу, настолько непостижима, что даже не волнует нас, не кажется нам чудом, и, даже больше, не существует для нас. Но бесконечность одного направления, имеющая начало, но неимеющая конца, или имеющая конец, но не имеющая начало, такая бесконечность потрясает нас. Она пронизывает нас своим концом или началом, и отрезок бесконечной прямой образующий хорду в кругу нашего сознания, с одной стороны постигается нами, а с другой стороны соединяет нас с бесконечным. Представить себе, что что то никогда не начиналось и никогда не кончится мы можем в искажённом виде. Этот вид таков: чтото никогда не начиналось, а потомуникогда и не кончится. Это представление о чём то есть представление ни о чём. Мы ставим связь между началом и концом и отсюда выводим первую теорему: что нигде не начинается, то нигде и не кончается, а что где то начинается, то гдето и кончается. Первое есть бесконечное, второе – конечное. Первое – ничто, второе-что-то».