Эндрю Макафи - Вторая эра машин. Работа, прогресс и процветание в эпоху новейших технологий

Одна из особенностей, отличающих вторую эру машин, – это скорость, с которой мы оказываемся на второй половине шахматной доски. Мы не хотим сказать, что в прежние времена никакие другие технологии не развивались по экспоненте. К примеру, после однократного резкого усовершенствования парового двигателя в результате инновации Уатта дополнительные мелкие изобретения привели к экспоненциальному улучшению в следующие 200 лет. Однако величина экспоненты была сравнительно небольшой, поэтому за весь период произошло лишь 3–4 удвоения эффективности. [72] См. http://www.cuug.ab.ca/~branderr/pmc/012_coal.html (по состоянию на 23 сентября 2013 г.). С такими темпами нам потребовалось бы целое тысячелетие для того, чтобы добраться до второй половины шахматной доски. В условиях второй эры машин удвоение происходит значительно быстрее, а экспоненциальный рост оказывается более заметным.

Наш быстрый расчет удвоений помогает понять, почему прогресс в области цифровых технологий все ускоряется и почему так много идей из области научной фантастики становятся реальностью бизнеса. Дело в том, что устойчивый и быстрый экспоненциальный рост закона Мура дошел до точки, с которой вычисления переходят в другой режим: мы теперь на второй половине шахматной доски. Инновации, описанные нами в предыдущей главе, – машины, способные самостоятельно передвигаться в дорожном потоке, суперкомпьютеры – чемпионы Jeopardy! , автоматически формируемые новости, дешевые и удобные фабричные роботы, а также недорогие потребительские устройства, представляющие собой одновременно коммуникаторы, «трикордеры» и компьютеры, – возникли после 2006 года, так же как и бесчисленное количество других диковин, совершенно непохожих на устройства прежних эпох.

Рис. 3.3.Множество измерений закона Мура

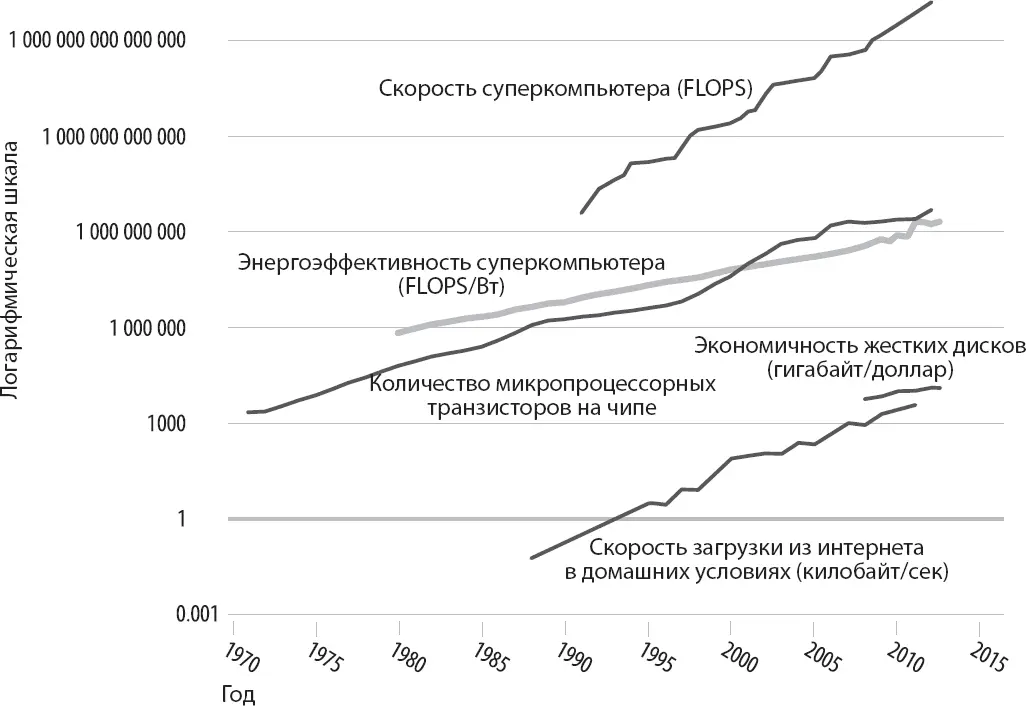
Одна из причин появления этих гаджетов состоит в том, что цифровой «движок», на котором они построены, наконец-то стал достаточно быстрым и при этом достаточно дешевым. Десять лет назад все было совсем иначе. Как выглядит цифровой прогресс на логарифмической шкале? Давайте посмотрим.

График на стр. 74 показывает, что закон Мура реализуется последовательно и широко; он действует в течение долгого времени (в некоторых случаях – десятилетия) и вполне применим к разным типам цифрового прогресса. Глядя на него, помните, что при использовании стандартной линейной шкалы на вертикальной оси все эти почти прямые линии напоминали бы первый график семейства трибблов Энди – они почти все время шли бы горизонтально, а затем, ближе к концу, взмывали бы вверх. И, конечно же, у вас не было бы никакой возможности изобразить их все вместе – все случаи описываются слишком разными по масштабу цифрами. Логарифмическая шкала принимает все это во внимание и позволяет нам получить более четкую общую картину изменений, связанных с цифровыми устройствами.

Вполне ясно, что многие существенно важные строительные блоки процесса вычислений: плотность микрочипов, скорость обработки, емкость запоминающего устройства, энергоэффективность, скорость загрузки и так далее – улучшались по экспоненте в течение долгого времени. Чтобы понять важность закона Мура для реального мира, давайте сравним возможности компьютеров, разделенных лишь несколькими периодами удвоений. Машина ASCI Red (1996), первый плод Ускоренной стратегической компьютерной инициативы ( Accelerated Strategic Computing Initiative ) правительства США, была на момент своего появления самым быстрым из когда-либо существовавших суперкомпьютеров. Для его создания потребовалось 55 миллионов долларов, а сотня его серверных шкафов занимала площадь почти в 150 квадратных метров в Национальной лаборатории Сандиа в штате Нью-Мексико. [73] Lonut Arghire, “The Petaflop Barrier Is Down, Going for the Exaflop?”, Softpedia, 10 июня 2008 г., http://news.softpedia.com/news/The-Petaflop-Barrier-Is-Down-Goingfor-the-exaflop-87688.shtml. Этот компьютер, предназначенный для расчета ресурсоемких задач типа имитации ядерных испытаний, был первым устройством, которое показало скорость выше одного терафлопа – то есть триллиона операций с плавающей запятой [74] Примером операции с плавающей запятой может служить умножение 62,34 на 24358,9274. Знак, отделяющий целую часть от дробной, в обоих числах может «плавать», а не оставаться в одной и той же позиции. в секунду – в ходе стандартных тестов. Чтобы достичь такой скорости, компьютеру требовалось более 800 киловатт в час, что сопоставимо с мощностью, потребляемой 800 домами. К 1997 году скорость ASCI Red достигла 1,8 терафлопа.