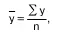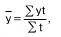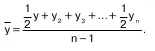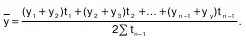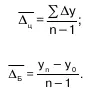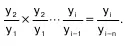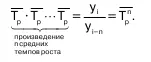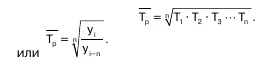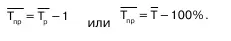Лидия Щербина - Общая теория статистики

Метод расчета среднего уровня ряда динамики зависит прежде всего от характера показателя, лежа–щего в основе ряда.

Наиболее просто исчисляется средний уровень интервального ряда динамики абсолютных величин с равностоящими уровнями. Расчет производится по формуле простой средней арифметической:

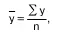
где n – число фактических уровней за последо–вательные равные отрезки времени.

Сложнее обстоит дело с исчислением среднего уровня моментного ряда динамики абсолютных вели–чин. Моментный показатель может изменяться почти непрерывно. Поэтому очевидно, что, чем более по–дробными и исчерпывающими данными о его измене–нии мы располагаем, тем более точно можно исчи–54б зависит от того, насколько подробны имеющиеся данные. Здесь возможны различные случаи.

При наличии исчерпывающих данных об измене–нии моментного показателя его средний уровень исчи–сляется по формуле средней арифметической взве–шенной для интервального ряда с разностоящими уровнями:

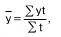
где t – число периодов времени, в течение которых уровень не изме–нялся.

Если промежутки времени между соседними да–тами равны друг другу, т. е. когда мы имеем дело с равными (или примерно равными) интервалами между датами, тогда для моментального ряда с рав–ностоящими уровнями расчет среднего уровня ряда производим по формуле средней хронологической:

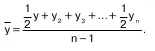
Для моментального ряда с разностоящими уров–нями расчет среднего уровня ряда производится по формуле:

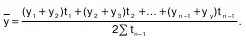
Выше шла речь о среднем уровне рядов динами–ки абсолютных величин. Для рядов динамики средних и относительных величин средний уровень нужно ис–числять исходя из содержания и смысла этих средних и относительных показателей.

Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уро–вень по сравнению с предыдущим в среднем за еди–ницу времени. Средний абсолютный прирост характе–ризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем. Он вычисляется путем деления общего прироста за весь период на длину этого периода в тех или иных единицах времени:

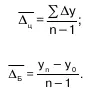
В качестве основы и критерия правильности ис–числения среднего темпа роста (как и среднего абсо–лютного прироста) можно использовать в роли опре–деляющего показателя произведение цепных темпов роста, которое равно темпу роста за весь рассматри–ваемый период. Таким образом, перемножив n цеп–ных темпов роста, получается темп роста за весь пе– риод:

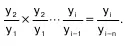
Должно соблюдаться равенство:

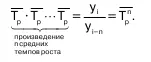
Данное равенство представляет формулу простой средней геометрической Из этого равенства следует:

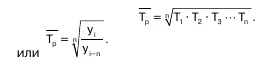
Средний темп роста, выраженный в форме коэф–фициента, показывает, во сколько раз увеличивался уровень по сравнению с предыдущим в среднем за единицу времени.

Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, которая имеет место между обычными темпами роста и прироста:

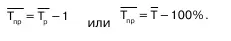
Средний темп прироста (или снижения), выра–женный в процентах, показывает, на сколько процен–тов увеличивался (или снижался) уровень по сравне–нию с предыдущим в среднем за единицу времени. Средний темп прироста характеризует среднюю ин–тенсивность роста.

Из двух видов формулы среднего темпа роста ча–ще используется вторая, так как она не требует вычи–сления всех цепных темпов роста. По первой формуле расчет целесообразно производить лишь в тех слу–чаях, когда не известны ни уровни ряда динамики, ни темп роста за весь период, а известны только цепные темпы роста (или прироста).