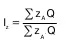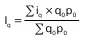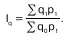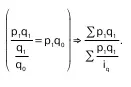Лидия Щербина - Общая теория статистики

При двусторонних сравнениях каждая террито–рия или объект с одинаковым основанием могут быть приняты как в качестве сравниваемого, так и в каче–стве базы сравнения. В связи с этим возникает вопрос о фиксировании весов сводного индекса на уровне того или иного района (объекта). Пусть, например, нужно определить, в какой из двух областей и на сколько процентов ниже себестоимость единицы про–дукции и больше объем ее производства.

Если сравнивать область А с областью Б, доста–точно обоснованный и простой путь состоит в том, чтобы зафиксировать в индексе себестоимости в ка–честве весов объемы продукции в целом по обеим территориям ( Q = Q A + Q B ), тогда получается:

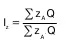
При многосторонних сравнениях, напри–мер при сравнениях качественных показателей по нескольким областям, нужно, соответственно, рас–ширить и границы территории, на уровне которой фик–сируются веса.

В сводных территориальных индексах объемных показателей в качестве весов могут быть приняты сред–ние уровни соответствующих качественных показате–лей, вычисленные в целом по сравниваемым террито–риям.

В зависимости от методологии расчета индивиду–альных и сводных индексов различают средние ариф–метические и средние гармонические индексы. Други–ми словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса.

Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне естественна, ведь сводный индекс является об–щей мерой, характеризующей среднюю величину изме–нения индексируемого показателя, и его величина дол–жна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного ин–декса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.

Преобразование агрегатного индекса в сред–ний из индивидуальных (групповых) индексов произ–водится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индек–сируемый показатель заменяется его выражени–ем через соответствующий индивидуальный ин–декс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в сред–ний гармонический из индивидуальных индексов.

Формула свободного индекса:

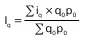
Средний арифметический индекс физического объема, где весами служит стоимость отдельных ви–дов продукции в базисном периоде.

В наличии имеется информация о динамике объема выпуска каждого вида продукции (i q) и стои–мости каждого вида продукции в отчетном пе–риоде (p 1q 1). Для определения общего измене–ния выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:

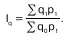
Числитель формулы можно получить суммирова–нием величин p 1q 1, а знаменатель – делением факти–ческой стоимости каждого вида продукции на соот–ветствующий индивидуальный индекс физического объема продукции, т. е. делением p 1q 1/ i q, тогда:

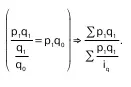
Таким образом получаем формулу среднего взвешенного гармонического индекса физического объема.

Применение той или иной формулы индекса фи–зического объема (агрегатного, среднего арифмети–ческого и среднего гармонического) зависит от имею–щейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразо–ван и рассчитан как средний из индивидуальных ин–дексов только при совпадении перечня видов продук–ции или товаров (их ассортимента) в отчетном и базис–ном периодах.

1. Предмет статистики – это сбор и обработка экономических показателей, позволяющих произво–дить анализ экономической деятельности предприя–тий различных типов и отраслей.

Сбор статистической информации по заказам конкретных потребителей осуществляется в рамках отраслевой статистики.

Вся информация разделена на два потока:

1) основные результаты всей экономической дея–тельности малых предприятий независимо от их отраслевой принадлежности;