Альфред Маршалл - Принципы экономической науки

Мы можем перейти теперь к его анализу влияния усовершенствований в ведении сельского хозяйства, которые он делит на два класса. Особый научный интерес представляет его рассмотрение первого из них, включающего улучшения, благодаря которым "...я могу получить тот же продукт, затратив меньший капитал и не нарушая разницы между производительностью последовательных долей капитала..." [Рикардо. Указ. соч., т. I, с. 75. Ср. с упомянутой выше работой Кэннана, с. 325-326. Разграничение Рикардо двух классов улучшений не во всем удачно, и рассматривать его здесь нет необходимости.], оставляя, конечно, в стороне в целях общего доказательства тот факт, что любое улучшение может оказать на один участок большее влияние, чем на другой (см. выше, кн. IV гл. III, § 4). Допуская, как и раньше, что спрос на зерно неэластичен, он утверждает, что капитал будет изъят из более бедных участков (и из более интенсивной обработки богатых участков), поэтому добавочная выгода, измеренная в зерне (дополнительная выгода зерна — нашим языком), которую приносит приложение капитала в наиболее благоприятных условиях, будет излишком по отношению к участкам, не настолько бедным, какими были до этого предельные участки; и поскольку, согласно принятым предпосылкам, различия в производительности любых двух вложений капитала остаются неизменными, дополнительная выгода зерна обязательно сократится, а реальная стоимость и трудовые издержки дополнительной выгоды, конечно же, снизятся гораздо больше, чем в той же пропорции.

Это можно пояснить графически. Кривая АС выражает отдачу земли всей страны, рассматриваемой как одна ферма, на дозы приложенного к ней капитала и труда; эти дозы расположены не по порядку их вложения, а по производительности. При условии равновесия вложены дозы капитала OD, а цена зерна такова, что отдача DC как раз достаточна для вознаграждения любой дозы; общее количество выращенного зерна представлено областью AODC, часть которой АНС представляет совокупную дополнительную выгоду зерна. [Мы можем отвлечься, чтобы заметить, что единственное изменение, которое потребуется внести при использовании этой диаграммы для описания всей страны не как единственной фермы, связано с тем, что в этом случае в отличие от предыдущего мы не можем предположить, что все дозы капитала вкладываются в непосредственной близости друг от друга, и поэтому, что стоимости одинаковых количеств продукта (одного сорта) равны. Правда, мы можем преодолеть это затруднение, включив расходы по доставке продукции на общий рынок в затраты на ее производство, так как определенная часть каждой дозы капитала и труда предназначена для расходов на доставку]

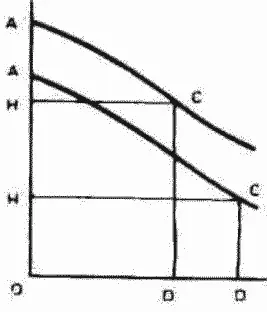
Допустим теперь, что одно из улучшений первого класса, по Рикардо, увеличивает отдачу на капитал, примененный в наиболее благоприятных условиях, с ОА до ОА , а на другие дозы капитала — не в одинаковой пропорции, а в одинаковых размерах. Результатом этого будет новая кривая продукта А'С'', в точности повторяющая старую кривую продукта АС, но расположенная выше на расстоянии АА'. Поэтому если спрос на зерно неограничен, что позволяет с прибылью применить старое число частей капитала, OD, то совокупная дополнительная выгода зерна останется такой же, как и до изменения. Однако на практике такое немедленное расширение производства не может быть прибыльным, поэтому улучшение такого рода должно обязательно снизить совокупную дополнительную выгоду зерна. И при допущении Рикардо для этого случая, что совокупная продукция не увеличится вовсе, будет применен только капитал OD, величина которого зависит от условия, что A'OD'Cf равно AODC, а совокупная добавочная выгода зерна сократится до A'H'C'. Этот результат независим от формы АС и — что то же самое — от конкретных чисел, избранных Рикардо для иллюстрации, которую он использовал в доказательстве своего вывода.

Мы имеем здесь повод заметить, что числовые примеры с уверенностью можно использовать, как правило, только для иллюстрации, но не как аргументы, поскольку узнать, не был ли результат неявно заложен в цифрах, приведенных к данному случаю, труднее, чем определить независимо от исчислений, верен результат или нет. Сам Рикардо не получил математического образования. Однако его чутье уникально, и очень немногие образованные математики могли бы проходить с такой же уверенностью наиболее рискованные повороты его доказательства. Даже проницательная логика Милля оказывалась недостаточной.