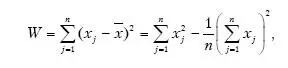Наталия Климова - Экономический анализ

Способ пропорционального деления используется для аддитивных и кратно-аддитивных моделей.

Алгоритм расчета количественного влияния исследуемого фактора на изменение результативного показателя для аддитивной модели:

• абсолютное изменение результативного показателя делится на сумму абсолютных изменений всех факторов;

• полученный результат умножается на абсолютное отклонение исследуемого фактора.

Пример: Y = х 1 + х 2 + х 3.

Изменение Yза счет фактора х 1 :

ΔYх 1= ΔY общ/(Δх 1+ Δх 2+ Δх 3) × Δх 1.

Изменение Y за счет фактора х 2 :

ΔYх 2= ΔY общ/(Δх 1+ Δх 2+ Δх 3) × Δх 2.

Изменение Y за счет факторах,

ΔYх 3= ΔY общ/(Δх 1+ Δх 2+ Δх 3) × Δх 3.

Сумма влияния факторов должна быть равна общему изменению результативного показателя.

Метод корреляционно-регрессионного анализа позволяет определить изменение результативного показателя под воздействием одного или нескольких факторов, т. е. определить, на сколько единиц изменяется величина результативного показателя при изменение факторного на единицу, а также позволяет установить относительную степень зависимости результативного показателя от каждого фактора. Корреляционная зависимость проявляется лишь в среднем (как среднее значение) и только в массе наблюдений.

Множественная корреляционная модель имеет вид:

y = а 0+ а 1х 1+ а 2х 2+ а 3х 3+ … + а nх n,

где у – результативный показатель; a Q – свободный член уравнения; а 1,2,3 и т.д. аргументы, показывающие, на сколько изменится результат при увеличении соответствующему ему х на единицу; x 1,2,3 и т. д.– факторы, воздействующие на результативный показатель.

Многофакторный корреляционный анализ состоит из нескольких этапов.

На первом этапе определяются факторы, которые оказывают влияние на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа.

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т. е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости.

На четвертом, этапе проводится расчет основных показателей связи корреляционного анализа.

На пятом этапе статистически оцениваются результаты корреляционного анализа и практическое их применение.

В последние годы наибольшую актуальность в практической деятельности приобрел такой метод изучения многомерных статистических совокупностей, как кластерный анализ, содержание которого было впервые раскрыто в 1939 г. исследователем Трионом.

Сущность кластерного анализа заключается в разбиении множества изучаемых объектов и признаков на однородные группы или кластеры. Достоинство данного метода в том, что он позволяет подразделять объекты не по одному параметру, а по целому ряду признаков и в отличие от большинства математико-статистических методов не накладывает никаких ограничений на рассматриваемые объекты.

Кластерный анализ позволяет рассматривать достаточно большой объем информации, сжимать массивы социально-экономической информации, делать их компактными и наглядными. Однако состав и количество кластеров зависят от выбираемых критериев разбиения. В то же время могут теряться индивидуальные черты отдельных объектов за счет замены их характеристиками обобщенных значений параметра кластера. Это следует отнести к недостатку кластерного анализа.

В процессе проведения кластерного анализа необходимо на основании данных, содержащихся во множестве X, разбить на множество объектов G на от (от целое) кластеров (подмножеств) Q 1, Q 2, … Q mтак, чтобы каждый объект G j принадлежал только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными.

В качестве целевой функции кластерного анализа может быть взята внутригрупповая сумма квадратов отклонения:

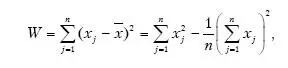
где х j представляет собой измерения j-го объекта.

Кластерный анализ можно применять к интервальным датам, частотам, при группировке данных, моделировании рыночной конъюнктуры. Способ сравнения применяется в следующих случаях.