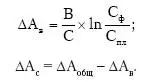Наталия Климова - Экономический анализ

ТП усл+ ΔТП ц= ΔТП общ.

Используя способ цепной подстановки, необходимо выполнить ряд правил:

• в первую очередь учитывается изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и качественных факторов, то сначала следует изменить факторы первого уровня подчинения, а потом второго;

• в расчетах количественного влияния факторов на результат обязательно используется условный показатель;

• фактические данные сравниваются с плановыми (или данные отчетного периода с базисными показателями).

Способ абсолютных разниц используется только в мультипликативных и смешанных моделях. При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на плановую (базовую) величину факторов, которые находятся справа от него, и на фактическую (отчетную) величину факторов, расположенных слева от него в модели.

Алгоритм, расчета:

1. Рассчитаем абсолютное изменение:

• объема реализации (ΔК):

ΔК = К ф – К пл;

• цены (ΔЦ):

2. Рассчитаем изменение выручки за счет:

• изменения количества проданной продукции (ΔТП к):

ΔТП к= ΔК х Ц пл;

• изменения цены реализации (ΔТП ц):

ΔТП ц= К фх ΔЦ.

3. Проверка расчетов:

ΔТП к+ ΔТП ц= ΔТП общ

Способ относительных разниц применяется в тех же моделях, что и при использовании метода абсолютных разниц. Он значительно проще цепных подстановок, что делает его более эффективным, особенно когда требуется рассчитать влияние более 8 факторов.

Алгоритм расчета:

1. Для расчета влияния первого фактора необходимо плановую (базисную) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100 %.

Изменение выручки за счет количества проданной продукции (ДТПк):

ΔТП к= (ТП плх ΔК%)/100 %;

ΔК% = (К ф – К пл)/К плх 100 %.

2. Чтобы рассчитать влияние второго фактора, необходимо к плановой величине результативного фактора прибавить изменение результативного показателя за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора в процентах и результат разделить на 100 %.

Изменение выручки за счет цены реализации (ΔТП ц):

ΔТП ц= (ТП пл+ ΔТП к) х ΔЦ%/100 %;

ΔЦ% = (Ц ф-Ц пл)/Ц плх100 %.

3. Влияние третьего, четвертого и т. д. факторов (при их наличии) определяется аналогично второму этапу с добавлением в сумму изменения результата за счет влияния второго, третьего и т. д. факторов.

4. Проверка расчетов:

ΔТП к+ ΔТП ц= ΔТП общ

Недостаток предыдущих методов состоит в том, что научно-технические факторы интенсификации производства не могут быть включены в модель прямых связей, а следовательно, их недоучет приведет к занижению или завышению отдельных результатов.

Вторым недостатком является зависимость результатов расчетов от того, насколько логически и экономически правильно составлена формула и, следовательно, могут быть сформулированы различные выводы.

Поэтому, прежде чем приступить к расчетам, необходимо:

• выявить четкую взаимосвязь между изучаемыми показателями (явлениями);

• разграничить количественные и качественные показатели;

• правильно определить последовательность подстановок в тех случаях, когда имеется несколько количественных и качественных показателей.

Интегральный метод имеет преимущества, заключающиеся в получении более точных результатов расчета влияния факторов по сравнению с другими методами и исключения неоднородной оценки влияния факторов. Это является следствием того, что результаты расчетов не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними пропорционально изолированному их воздействию на результативный показатель.

Интегральный метод применяется в мультипликативных, кратных и смешанных моделях с использованием для каждой из них определенных формул.

1. Для двухфакторных мультипликативных моделей.

Пример: ТП = К х Ц.

Расчет изменения выручки за счет:

• количества проданной продукции (ΔТП к):

ΔТП к=1/2К х (Ц пл+ Ц ф);

• цены реализации (ΔТП ц):

ΔТП ц=1/2Ц х (К пл+ К ф).

2. Для кратной двухфакторной модели: А = В/С.

ΔА общ= А ф – А пл;

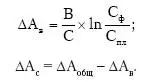
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. При логарифмировании используются не абсолютные приросты результативных показателей, а индексы их роста или снижения. Общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя.