Литагент HarperCollins - The Ultimate Mathematical Challenge - Over 365 puzzles to test your wits and excite your mind

[SOLUTION]

16. Sums of digits

For how many three-digit numbers does the sum of the digits equal 25?

[SOLUTION]

17. A million seconds

How many days, to the nearest day, are there in a million seconds?

[SOLUTION]

18. Sum to 100

The sum of 10 distinct positive integers is 100. What is the largest possible value of any of the 10 integers?

[SOLUTION]

19. x marks the spot

The numbers 2, 3, 4, 5, 6, 7, 8 are to be placed, one per square, in the diagram shown such that the four numbers in the horizontal row add up to 21 and the four numbers in the vertical column also add up to 21.

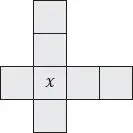
Which number should replace x ?

[SOLUTION]

20. The last Wednesday

One of the months in a particular year has five Wednesdays, and the third Saturday is the 19th.

Which day of the month is the last Wednesday?

[SOLUTION]

21. Her brother’s age

A woman says to her brother, ‘I am four times as old as you were when I was the same age as you are now.’

The woman is 40 years old.

How old is her brother now?

[SOLUTION]

Week 4

22. Pings and pongs

Five pings and five pongs are worth the same as two pongs and eleven pings.

How many pings is a pong worth?

[SOLUTION]

23. How many sides?

A single polygon is made by joining dots in the grid with straight lines, which meet only at dots at their end points. No dot is at more than one corner. The diagram shows a five-sided polygon formed in this way.

What is the greatest possible number of sides of a polygon formed by joining the dots using these same rules?

[SOLUTION]

24. A tennis club

Three-quarters of the junior members of a tennis club are boys and the rest are girls. What is the ratio of boys to girls among these members?

[SOLUTION]

25. Rectangles in a square

Five equal rectangles are placed inside a square with side length 24 cm, as shown in the diagram.

What is the area in cm 2of one rectangle?

[SOLUTION]

26. The absent present

Four children bought a birthday present for their father. One of the children hid the present. When their mother asked them who had hidden the present, the four children made the following statements:

Alfred: ‘It was not me!’

Benjamin: ‘It was not me!’

Christian: ‘It was Daniel!’

Daniel: ‘It was Benjamin!’

It turned out that exactly one of them did not tell the truth.

Who hid the present?

[SOLUTION]

27. Professor Brainstorm’s clock

Professor Brainstorm’s clock gains 16 minutes every day.

After she has set it to the correct time, how many days pass before it next tells the correct time?

[SOLUTION]

28. What is n?

You are given that n is a positive integer with the property that when we add n and the sum of its digits, we obtain the number 313.

What are the possible values of n ?

[SOLUTION]

Crossnumber 1

A crossnumber works just like a crossword except that, instead of filling each square with one of the letters from A to Z, you have to fill each square with a single digit from 0 to 9.

ACROSS

1. The square of an odd number (2)

3. 18 DOWN divided by six (3)

6. A number divisible by three (3)

7. A factor of 14 ACROSS (3)

9. An odd number that is one more than a cube (2)

10. One more than a number divisible by nine (2)

12. A number divisible by both six and a square greater than one (3)

14. A multiple of 7 ACROSS (3)

16. The sum of twice 1 ACROSS and 14 (2)

18. Seven less than a square (2)

19. One more than three times 6 ACROSS (3)

21. A Fibonacci number divisible by seven (3)

22. A palindrome that is twice a prime (3)

23. (9 ACROSS × 4) − 13 DOWN (2)

DOWN

2. A palindrome (3)

3. (3 × 9 ACROSS) − (1 ACROSS + 23 ACROSS) (3)

4. The product of two primes (2)

5. One less than a perfect number (2)

8. A cube that is also a power of two (3)

9. A factor of 6111 (3)

11. The sum of the digits of 8 DOWN and 21 ACROSS (2)

12. A number divisible by four (2)

13. A prime that is also a Fibonacci number (3)

15. Three times a prime and six greater than a square (3)

17. One less than a multiple of nine (3)

18. A number divisible by three (3)

19. (12 DOWN × 2) − 5 (2)

20. The sum of the digits of 14 ACROSS is one more than twice the sum of the digits of this number (2)

[SOLUTION]

Week 5

29. Turbo the tortoise

Usain runs twice as fast as his mum. His mum runs five times as fast as his pet tortoise, Turbo. They all set off together for a run down the same straight path.

When Usain has run 100 metres, how far apart are his mum and Turbo the tortoise?

[SOLUTION]

30. Rolling a cube

A cube is being rolled on a plane so it turns around its edges. Its bottom face passes through the positions 1, 2, 3, 4, 5, 6 and 7 in that order, as shown.

Which of these two positions were occupied by the same face of the cube?

[SOLUTION]

31. Small change

My bus fare is 44p. If the driver can give me change, what is the smallest number of coins that must change hands when I pay this fare?

[The coins available are 1p, 2p, 5p, 10p, 20p, 50p, £1 and £2.]

[SOLUTION]

32. Eight factors

The number 78 has exactly eight factors, including 1 and 78.

Which is the smallest integer greater than 78 that has eight factors?

[SOLUTION]

33. A small sum

In the addition sum ‘ TAP ’ + ‘ BAT ’ + ‘ MAN ’, each letter must represent a different digit and no first digit is zero.

What is the smallest sum that can be obtained?

[SOLUTION]

34. A circle on a grid

A circle is added to the grid shown.

What is the largest number of dots that the circle can pass through?

[SOLUTION]

35. Numbers around a circle

Five integers are written around a circle in such a way that no two or three consecutive numbers have a sum that is a multiple of 3. Of the five numbers, how many are themselves multiples of 3?

[SOLUTION]

Week 6

36. Digit sum 2001

Which is the smallest positive integer whose digits add up to 2001?

[SOLUTION]

37. Seven semicircular arcs

The diagram shows a curve made from seven semicircular arcs, the radius of each of which is 1 cm, 2 cm, 4 cm or 8 cm.

What is the length of the curve?

[SOLUTION]

38. Sorting dominoes

Dominoes are said to be arranged correctly if, for each pair of adjacent dominoes, the numbers of spots on the adjacent ends are equal. Paul laid six dominoes in a line, as shown in the diagram.