Литагент HarperCollins - The Ultimate Mathematical Challenge - Over 365 puzzles to test your wits and excite your mind

Junior Problems , Andrew Jobbings, UKMT, 2017

Intermediate Problems , Andrew Jobbings, UKMT, 2016

Senior Problems , Andrew Jobbings, UKMT, 2018

In addition, both short and extended solutions for all the Challenge papers for recent years, which include questions for further investigations, may be downloaded for free from the UKMT website.

Mathematical Olympiad

The following books give advice about tackling harder problems at different levels, and include the problems and solutions from different Olympiad competitions, as specified.

First Steps for Problem Solvers , Mary Teresa Fyfe and Andrew Jobbings, UKMT, 2015 – includes all the problems, with solutions, from the Junior Mathematical Olympiad papers from 1999 to 2015.

A Problem Solver’s Handbook , Andrew Jobbings, UKMT, 2013 – includes all the problems, with solutions, from the Intermediate Mathematical Olympiad papers from 2003 to 2012.

A Mathematical Olympiad Primer , 2nd edition, Geoff Smith, UKMT, 2011 – includes all the problems, with solutions, from the British Mathematical Olympiad Round 1 papers from 1996 to 2010.

A Mathematical Olympiad Companion , Geoff Smith, UKMT, 2016 – includes all the problems, with solutions, from the British Mathematical Olympiad Round 2 papers from 2002 to 2016.

The Problems

Week 1

1. How many van loads?

A transport company’s vans each carry a maximum load of 12 tonnes. A firm needs to deliver 24 crates each weighing 5 tonnes.

How many van loads will be needed to do this?

[SOLUTION]

2. An L-ish puzzle

Beatrix places copies of the L-shape shown on a 4 × 4 board so that each L-shape covers exactly three cells of the board.

She is allowed to turn around or turn over an L-shape.

What is the largest number of L-shapes she can place on the board without overlaps?

[SOLUTION]

3. Granny’s meter

Yesterday, the reading on Granny’s electricity meter was 098657. She was shocked to realise that all six of these digits are different.

How many more units of electricity will she use before the next time all the digits are different?

[SOLUTION]

4. Paper folding

Three shapes X , Y and Z are shown below.

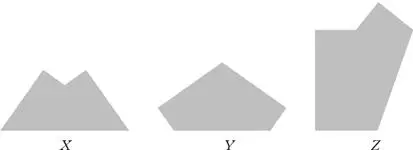
A sheet of A4 paper (measuring 297 mm × 210 mm) is folded once and placed flat on the table.

Which of these shapes could be made?

[SOLUTION]

5. How many triangles?

In total, how many triangles of any size are there in the diagram?

[SOLUTION]

6. Four dice

Rory uses four identical standard dice to build the solid shown in the diagram.

Whenever two dice touch, the numbers on the touching faces are the same. The numbers on some of the faces of the solid are shown.

What number is written on the face marked with an asterisk?

(On a standard dice, the numbers on opposite faces add to 7.)

[SOLUTION]

7. Making 73

Taran thought of a whole number and then multiplied it by either 5 or 6. Krishna added 5 or 6 to Taran’s answer. Finally Eshan subtracted either 5 or 6 from Krishna’s answer.

The final result was 73. What number did Taran choose?

[SOLUTION]

Week 2

8. Decimal time

In the late eighteenth century, a decimal clock was proposed in which there were 100 minutes in each hour and 10 hours in each day.

Assuming that such a clock started at 0.00 at midnight, what time would it show when an ordinary clock showed 6 o’clock the following morning?

[SOLUTION]

9. One size fits all

Harry’s mathematical grandmother keeps a large bag of ‘one size fits all’ socks in a dark cupboard. There are socks in red, blue, pink and green.

How many socks must she pull out to be sure of having a matching pair?

[SOLUTION]

10. Cut the net

The diagram represents a rectangular fishing net made from ropes knotted together at the points shown.

The net is cut several times; each cut severs precisely one section of rope between two adjacent knots.

What is the largest number of such cuts that can be made without splitting the net into two separate pieces?

[SOLUTION]

11. Times are changing

On a digital clock displaying hours, minutes and seconds, how many times in each 24-hour period do all six digits change simultaneously?

[SOLUTION]

12. Making axes

In the addition sum shown, each letter represents a different non-zero digit.

What digit does each letter represent?

[SOLUTION]

13. Roundabout

Four cars enter a roundabout at the same time, each one from a different direction, as shown in the diagram.

Each car drives in a clockwise direction and leaves the roundabout before making a complete circuit. No two cars leave the roundabout by the same exit.

How many different ways are there for the cars to leave the roundabout?

[SOLUTION]

14. True or false?

None of these statements is true.

Exactly one of these statements is true.

Exactly two of these statements are true.

All of these statements are true.

How many of the statements in the box are true?

[SOLUTION]

Logic Challenge 1

The team photograph

A photograph is to be taken of the school mixed five-a-side football squad, which includes three substitutes. The girls in the squad are Liz, Jenny, Sarah and Tracey. The boys are Alan, Matthew, Peter and Steve.

The team line up in two rows of four. Read the clues below to work out who is standing where and what number they are wearing (which will be one of the numbers from 1 to 8).

Place the number in the top square of the answer grid and the name in the bottom square of each row.

The clues

Tracey is in the front row in front of Jenny.

The average of the two numbers in the middle of the front row is Sarah’s number, a square.

Peter is not sitting next to a girl.

Steve is sitting between Liz and Jenny.

Players with prime numbers, which includes Alan, are sitting in the front row.

There is only one boy on the end of a row.

In both the front and back rows the two places on the right (as you look at it) are filled by a boy and a girl.

Matthew and Steve have the highest and lowest numbers a boy could wear.

Jenny’s number is three times as large as Tracey’s and twice as large as that of Peter, who is not sitting on the end of a row.

Girls have even numbers.

Back row

Front row

[SOLUTION]

Week 3

15. A line of lamp posts

Four lamp posts are in a straight line. The distance from each post to the next is 25 metres.

What is the distance from the first post to the last?