The ancient Greeks also liked to attribute sexual qualities to numbers, but it was they who first discovered, in the 4th century BC, the primes’ true potency as the building blocks for all numbers. They saw that every number could be constructed by multiplying prime numbers together. Whilst the Greeks mistakenly believed fire, air, water and earth to be the building blocks of matter, they were spot on when it came to identifying the atoms of arithmetic. For many centuries, chemists strove to identify the basic constituents of their subject, and the Greeks’ intuition finally culminated in Dmitri Mendeleev’s Periodic Table, a complete description of the elements of chemistry. In contrast to the Greeks’ head start in identifying the building blocks of arithmetic, mathematicians are still floundering in their attempts to understand their own table of prime numbers.
The librarian of the great ancient Greek research institute in Alexandria was the first person we know of to have produced tables of primes. Like some ancient mathematical Mendeleev, Eratosthenes in the third century BC discovered a reasonably painless procedure for determining which numbers are prime in a list of, say, the first 1,000 numbers. He began by writing out all the numbers from 1 to 1,000. He then took the first prime, 2, and struck off every second number in the list. Since all these numbers were divisible by 2, they weren’t prime. He then moved to the next number that hadn’t been struck off, namely 3. He then stuck off every third number after 3. Since these were all divisible by 3, they weren’t prime either. He kept doing this, just picking up the next number which hadn’t already been struck from the list and striking off all the numbers divisible by the new prime. By this systematic process he produced tables of primes. The procedure was later christened the sieve of Eratosthenes . Each new prime creates a ‘sieve’ which Eratosthenes uses to eliminate non-primes. The size of the sieve changes at each stage, but by the time he reaches 1,000 the only numbers to have made it through all the sieves are prime numbers.
When Gauss was a young boy he was given a present – a book containing a list of the first several thousand prime numbers which had probably been constructed using these ancient number sieves. To Gauss, these numbers just tumbled around randomly. Predicting the elliptical path of Ceres would be difficult enough. But the challenge posed by the primes had more in common with the near-impossible task of analysing the rotation of bodies such as Hyperion, one of Saturn’s satellites, which is shaped like a hamburger. In contrast to the Earth’s Moon, Hyperion is far from gravitationally stable and spins chaotically. Even though the spinning of Hyperion and the orbits of some asteroids are chaotic, at least it is known that their behaviour is determined by the gravitational pull of the Sun and the planets. But for the primes, no one had the faintest idea what was pulling and pushing these numbers around. As he gazed at his table of numbers, Gauss could see no rule that told him how far to jump to find the next prime. Were mathematicians just going to have to accept these numbers as determined by Nature, set like stars in the night sky with no rhyme or reason? Such a position was unacceptable to Gauss. The primary drive for the mathematician’s existence is to find patterns, to discover and explain the rules underlying Nature, to predict what will happen next.
The mathematician’s quest for primes is captured perfectly by one of the tasks we have all faced at school. Given a list of numbers, find the next number. For example, here are three challenges:
1, 3, 6, 10, 15, …
1, 1, 2, 3, 5, 8, 13, …
1, 2, 3, 5, 7, 11, 15, 22, 30, …
Numerous questions spring to the mathematical mind when faced with such lists. What is the rule behind the creation of each list? Can you predict the next number on the list? Can you find a formula that will produce the 100th number on the list without having to calculate the first 99 numbers?
The first sequence of numbers above consists of what are called the triangular numbers . The tenth number on the list is the number of beans required to build a triangle with ten rows, starting with one bean in the first row and ending with ten beans in the last row. So the N th triangular number is got by simply adding the first N numbers: 1 + 2 + 3 + … + N . If you want to find the 100th triangular number, there is a long laborious method in which you attack the problem head on and add up the first 100 numbers.
Indeed, Gauss’s schoolteacher liked to set this problem for his class, knowing that it always took his students so long that he could take forty winks. As each student finished the task they were expected to come and place their slate tablets with their answer written on it in a pile in front of the teacher. While the other students began labouring away, within seconds the ten-year-old Gauss had laid his tablet on the table. Furious, the teacher thought that the young Gauss was being cheeky. But when he looked at Gauss’s slate, there was the answer – 5,050 – with no steps in the calculation. The teacher thought that Gauss must have cheated somehow, but the pupil explained that all you needed to do was put N = 100 into the formula and you will get the 100th number in the list without having to calculate any other numbers on the list on the way.
Rather than tackling the problem head on, Gauss had thought laterally. He argued that the best way to discover how many beans there were in a triangle with 100 rows was to take a second similar triangle of beans which could be placed upside down on top of the first triangle. Now Gauss had a rectangle with 101 rows each containing 100 beans. Calculating the total number of beans in this rectangle built from the two triangles was easy: there are in total 101 × 100 = 10,100 beans. So one triangle must contain half this number, namely 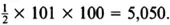 . There is nothing special here about 100. Replace it by N and you get the formula
. There is nothing special here about 100. Replace it by N and you get the formula 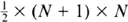 .
.
The picture overleaf illustrates the argument for the triangle with 10 rows instead of 100.
Instead of directly attacking his teacher’s problem, Gauss had found a different angle from which to view the calculation. Lateral thinking, turning the problem upside down or inside out to see it from a new perspective, is an immensely important theme in mathematical discovery and is one reason why people who can think like the young Gauss make good mathematicians.
The second challenge sequence, 1, 1, 2, 3, 5, 8, 13, …, consists of the so-called Fibonacci numbers . The rule behind this sequence is that each new number is calculated by adding the two previous ones, for example, 13 = 5 + 8. Fibonacci, a mathematician in the thirteenth-century court in Pisa, had struck upon the sequence in relation to the mating habits of rabbits. He had tried to bring European mathematics out of the Dark Ages by proselytising the discoveries of Arabic mathematicians. He failed. Instead, it was the rabbits that immortalised him in the mathematical world. His model of the propagation of rabbits predicted that each new season would see the number of pairs of rabbits grow in a certain pattern. This pattern was based on two rules: each mature pair of rabbits will produce a new pair of rabbits each season, and each new pair will take one season to reach sexual maturity.
Читать дальше

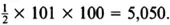 . There is nothing special here about 100. Replace it by N and you get the formula
. There is nothing special here about 100. Replace it by N and you get the formula 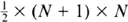 .
.










