Marcus Sautoy - The Music of the Primes - Why an unsolved problem in mathematics matters

To reveal quite how stunning Gauss’s pattern was, we can look at a graph of the function π( N ) counting the number of primes from 1 to N . Here’s a graph of π( N ) for numbers N from 1 to 100:

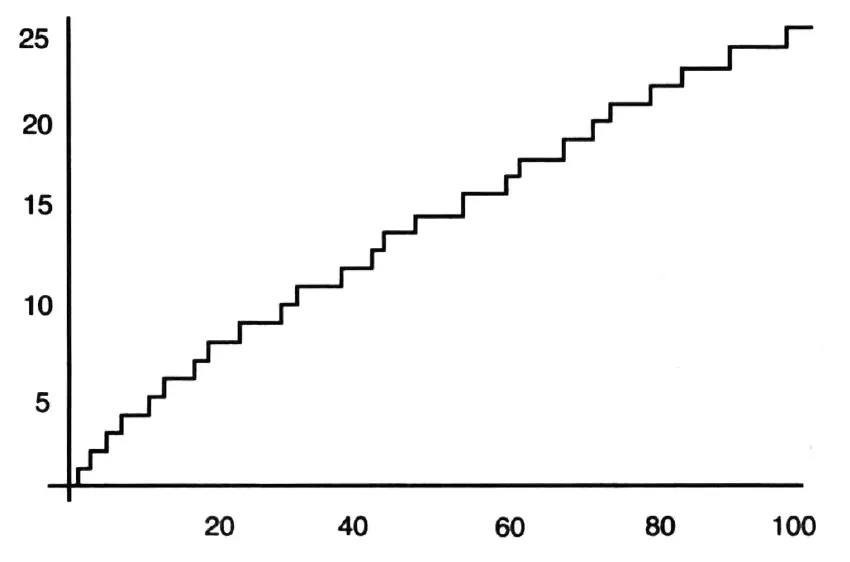
The prime number staircase – the graph counts the cumulative number of primes up to 100.

On this small scale the result is a jumpy staircase, where it is hard to predict how long one has to wait for the next step to appear. We are still seeing at this scale the minutiae of the primes, the individual notes.

Now step back and look at the same function where N is taken over a much wider range of numbers, say counting the primes up to 100,000.

The prime number staircase counting primes up to 100,000.

The individual steps themselves become insignificant and we end up seeing the overarching trend of this function creeping up. This was the big theme that Gauss had heard and could imitate using the logarithm function.

The revelation that the graph appears to climb so smoothly, even though the primes themselves are so unpredictable, is one of the most miraculous in mathematics and represents one of the high points in the story of the primes. On the back page of his book of logarithms, Gauss recorded the discovery of his formula for the number of primes up to N in terms of the logarithm function. Yet despite the importance of the discovery, Gauss told no one what he had found. The most the world heard of his revelation were the cryptic words, ‘You have no idea how much poetry there is in a table of logarithms.’

Why Gauss was so reticent about something so momentous is a mystery. It is true that he had only found early evidence of some connection between primes and the logarithm function. He knew that he had absolutely no explanation or proof of why these two things should have anything to do with each other. It wasn’t clear that this pattern might not suddenly disappear as you counted higher. Gauss’s reluctance to announce unproved results marked a turning point in mathematical history. Although the Greeks had introduced the idea of proof as an important component of the mathematical process, mathematicians before Gauss’s time were much more interested in scientific speculation about mathematics. If the mathematics worked, they weren’t too concerned about a rigorous justification of why it worked. Mathematics was still the tool of the other sciences.

Gauss broke from the past by stressing the value of proof. For him, presenting proofs was the primary goal of the mathematician, an ethos which has remained fundamental to this day. Without a proof of the connection between logarithms and primes, Gauss’s discovery was worthless to him. The freedom that the patronage of the Duke of Brunswick permitted him meant he could be quite choosy, almost indulgent about the mathematics he produced. His prime motivation was not fame and recognition but a personal understanding of the subject he loved. His seal bore the motto Pauca sed matura (‘Few but ripe’). Unless a result had reached full maturity it remained an entry in his diary or a doodle at the back of his table of logarithms.

For Gauss, mathematics was a private pursuit. He even encrypted entries in his diary using his own secret language. Some of them are easy to unravel. For example, on July 10, 1796, Gauss wrote Archimedes’ famous declaration ‘Eureka!’ followed by the equation

num = Δ + Δ + Δ

which represents his discovery that every number can be written as the sum of three numbers from the list of triangular numbers, 1, 3, 6, 10, 15, 21, 28, …, those numbers for which Gauss had produced his schoolroom formula. For example, 50 = 1 + 21 + 28. But other entries remain a complete mystery. No one has been able to unravel what Gauss meant when he wrote on October 11, 1796, ‘Vicimus GEGAN’. Some have blamed Gauss’s failure to disseminate his discoveries for holding back the development of mathematics by half a century. If he had bothered to explain half of what he had discovered and not been so cryptic in the explanations he did offer, mathematics might have advanced at a quicker pace.

Some people believe that Gauss kept his results to himself because the Paris Academy had rejected his great treatise on number theory, Disquisitiones Arithmeticae , as obscure and dense. Having been stung by rejection, to protect himself from any further humiliation he insisted that every last piece of the mathematical jigsaw be in place before he would consider publishing anything. Disquisitiones Arithmeticae did not receive immediate acclaim partly because Gauss continued to be cryptic even in the work he did expose to public view. He always claimed that mathematics was like a piece of architecture. An architect never leaves the scaffolding for people to see how the building was constructed. This was not a philosophy that helped mathematicians to penetrate Gauss’s mathematics.

But there were other reasons why Paris was not as receptive to Gauss’s ideas as he had hoped. By the end of the eighteenth century, mathematics in Paris was becoming ever more dedicated to serving the demands of an increasingly industrialised state. The Revolution of 1789 had shown Napoleon the need for a more centralised teaching of military engineering, and he responded by founding the École Polytechnique to further his war aims. ‘The advancement and perfection of mathematics are intimately connected with the prosperity of the State,’ Napoleon declared. French mathematics was dedicated to solving problems of ballistics and hydraulics. But despite this emphasis on the practical needs of the state, Paris still boasted some of the leading pure mathematicians in Europe.

One of the great authorities in Paris was Adrien-Marie Legendre, who was born twenty-five years before Gauss. Portraits of Legendre depict a rather puffed-up gentleman with a round, chubby face. In contrast to Gauss, Legendre came from a wealthy family but he had lost his fortune during the Revolution and been forced to rely instead on his mathematical talents for his livelihood. He too was interested in the primes and number theory, and in 1798, six years after Gauss’s childhood calculations, he announced his discovery of the experimental connection between primes and logarithms.

Although it would later be proved that Gauss had indeed beaten Legendre to the discovery, Legendre did nonetheless improve on the estimate for the number of primes up to N . Gauss had guessed that there were roughly N /log( N ) primes up to N . Although this was close, it was found to gradually drift away from the true number of primes as N got larger and larger. Here is a comparison of Gauss’s childhood guess, shown as the lower plot, with the true number of primes, the upper plot:

A comparison between Gauss’s guess and the true number of primes.

This graph reveals that although Gauss was on to something, there still seemed to be room for improvement.

Legendre’s improvement was to replace the approximation N /log( N ) by

thus introducing a small correction which had the effect of shifting Gauss’s curve up towards the true number of primes. As far as the values of these functions that were then within computational reach, it was impossible to distinguish the two graphs of π( N ) and Legendre’s estimate. Legendre, steeped in the prevailing preoccupation with the practical application of mathematics, was much less reluctant to stick his neck out and make some prediction about the connection between primes and logarithms. He was not a man scared to circulate unproven ideas, or even proofs with gaps in them. In 1808 he published his guess at the number of primes in a book about number theory entitled Théorie des Nombres .