Bhisham C. Gupta - Statistics and Probability with Applications for Engineers and Scientists Using MINITAB, R and JMP
Здесь есть возможность читать онлайн «Bhisham C. Gupta - Statistics and Probability with Applications for Engineers and Scientists Using MINITAB, R and JMP» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Statistics and Probability with Applications for Engineers and Scientists Using MINITAB, R and JMP
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Statistics and Probability with Applications for Engineers and Scientists Using MINITAB, R and JMP: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Statistics and Probability with Applications for Engineers and Scientists Using MINITAB, R and JMP»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Statistics and Probability with Applications for Engineers and Scientists using MINITAB, R and JMP, Second Edition Features two new chapters—one on Data Mining and another on Cluster Analysis Now contains R exhibits including code, graphical display, and some results MINITAB and JMP have been updated to their latest versions Emphasizes the p-value approach and includes related practical interpretations Offers a more applied statistical focus, and features modified examples to better exhibit statistical concepts Supplemented with an Instructor's-only solutions manual on a book’s companion website
is an excellent text for graduate level data science students, and engineers and scientists. It is also an ideal introduction to applied statistics and probability for undergraduate students in engineering and the natural sciences.

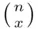 is usually called binomial coefficient , since it appears in the binomial expansion (for integer
is usually called binomial coefficient , since it appears in the binomial expansion (for integer 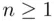 )
)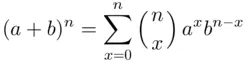
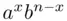 in the expansion of
in the expansion of 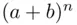 is
is 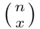 , since we can write
, since we can write 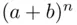 as
as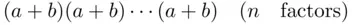
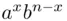 is the number of ways to pick x of these factors and then choose a from each factor, while taking b from the remaining
is the number of ways to pick x of these factors and then choose a from each factor, while taking b from the remaining 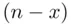 factors.
factors.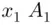 's,
's, 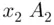 's, …,
's, …, 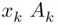 's, where
's, where  . Then total number of distinguishable arrangements of these several kinds of A's denoted by
. Then total number of distinguishable arrangements of these several kinds of A's denoted by 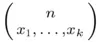 is
is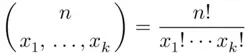
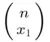 ways of choosing
ways of choosing 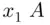 's to be replaced by
's to be replaced by 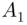 's. In each of these
's. In each of these 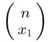 ways, there are
ways, there are 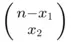 ways of choosing
ways of choosing 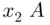 's to be replaced by
's to be replaced by 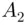 's. Hence, the number of ways of choosing
's. Hence, the number of ways of choosing 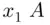 's and replacing them with
's and replacing them with 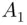 's and choosing
's and choosing 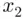 from the remaining
from the remaining 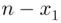 A 's and replacing them with
A 's and replacing them with 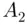 's is
's is 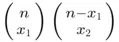 . Continuing this argument and using equation ( 3.4.4) shows that the number of ways of choosing
. Continuing this argument and using equation ( 3.4.4) shows that the number of ways of choosing 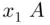 's and replacing them with
's and replacing them with 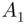 's,
's, 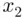 A 's and replacing them with
A 's and replacing them with 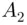 's, and so on until the last
's, and so on until the last 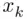 A 's replaced with
A 's replaced with 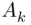 's, is
's, is