Robert G. Reynolds - Cultural Algorithms

2 Cultural Algorithms inherently support population co‐evolution. Stress within the social fabric can naturally produce co‐evolving populations. New links can be created subsequently to allow the separate populations to interact again.

3 Cultural Algorithms also support alternative ways to use resources through the emergence of subcultures. A subculture is defined as a culture contained within a broader mainstream culture, with its own set of goals, values, practices, and beliefs. Just as co‐evolution concerns the disconnection of individuals in the agent network, subcultures represent a corresponding separation of knowledge sources in the Belief Space into subcomponents that are linked to groups of connected individuals within the Population Space.

4 Cultural Algorithms support the social context of an individual by providing mechanisms for that individual to resolve conflicts with other individuals in the population space through the use of knowledge distribution mechanisms. These mechanisms are designed to reduce conflicts between individuals through the sharing of knowledge sources that influence them. This practice can be used to modulate the flow of knowledge through the population. The use of certain distribution strategies can produce viral distributions of information on the one hand or slow down the flows of the other knowledge sources dependent on the context. This feature makes it a useful learning mechanism with regards to design of systems that involve teams of agents.

5 Cultural Algorithms support the idea of a networked performance space. That is, the performance environment can be viewed as a connected collection of performance functions or performance simulators. This allows agent performance to potentially modify performance assessment and expectations.

6 Cultural Algorithms can exhibit the flexibility needed to cope with the changing environments in which they are embedded. They were in fact developed to learn about how social systems evolved in complex environments [3].

7 Cultural Algorithms facilitate the development of distributed systems and their supporting algorithms. The knowledge‐intensive nature of cultural systems requires the support of both distributed and parallel algorithms in the coordination of agents and their use of knowledge.

All of these features have been observed to emerge in one or more of the various Cultural Algorithm systems that have been developed over the years. In subsequent chapters of this book, we will provide examples of these features as they have emerged and their context.

While there is wide variety of ways in which Cultural Algorithms can be implemented, there is a general metaphor that describes the learning process in all of them. The metaphor is termed the “Cultural Engine.” The basic idea is that the new ideas generated in the Belief Space by the incorporation of new experiences into the existing knowledge sources produce the capacity for changes in behavior. This capacity can be viewed as entropy in a thermodynamic sense. The influence function in conjunction with the knowledge distribution function can then distribute this potential for variation through the network of agents in the Population Space. Their behaviors taken together provide a potential for new ideas that is then communicated to the Belief Space and the cycle continues.

We can express the Cultural Algorithm Engine in terms of the entropy‐based laws of thermodynamics. The basic laws of classical thermodynamic concerning systems in equilibrium are given below [4]:

If two thermodynamic systems are separately in thermal equilibrium with a third, they are also in thermal equilibrium with each other. If we assume that all systems are (trivially) in thermal equilibrium with themselves, the Zeroth law implies that thermal equilibrium is an equivalence relation on the set of thermodynamic systems. This law is tacitly assumed in every measurement of temperature.

The change in the internal energy of a closed thermodynamic system is equal to the sum of the amount of heat energy supplied to or removed from the system and the work done on or by the system.

The total entropy of any isolated thermodynamic system always increases over time, approaching a maximum value. Therefore, the total entropy of any isolated thermodynamic system never decreases.

As a system asymptotically approaches absolute zero of temperature, all processes virtually cease, and the entropy of the system asymptotically approaches a minimum value.

We metaphorically view our Cultural Algorithm as composed of two systems, a Population of individual agents moving over a performance landscape as well as a collection of knowledge sources in the Belief Space. Each of the knowledge sources can be viewed statistically as a bounding box or generator of control. If we look closely at the second law, it states that over time an individual system will always tend to increase its entropy. Thus, over time the population should randomly spread out over the surface and the bounding box for each knowledge source expand to the edge of the surface, encompassing the entire surface. Yet this does not happen here. This can be seen in terms of a contradiction posed by Maxwell relative to the second law. This Contradiction is the basis for Maxwell's Demon.

In the 1860s, the Physician Maxwell devised a thought experiment to refute the second law [5]. The basis for this refutation was that the human mind was different than pure physical systems and that the universe need not run down as predicted by the second law. In his thought experiment, there were two glass boxes. Within each box was a collection of particles moving at different rates. There was a trap door connecting the boxes controlled by a demon, see Figure 1.2. This demon was able to selectively open the door to “fast” particles from A and allow them to go to B. Therefore, increasing the entropy of B and reducing that of A.

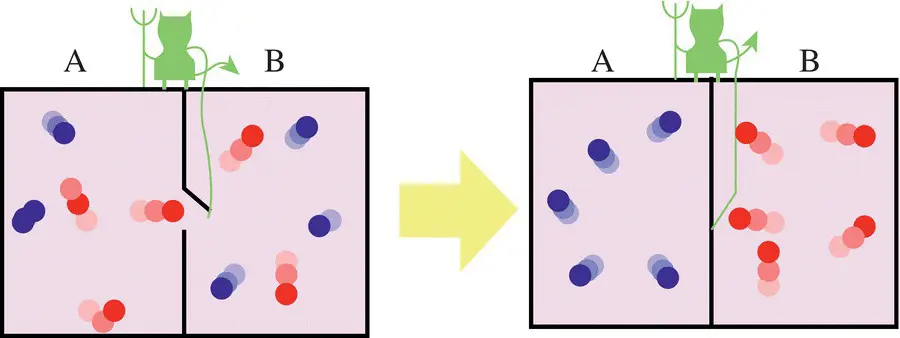
Figure 1.2 An example of Maxwell's demon in action. The demon selectively lets particles of high entropy from one system to another. Reducing the entropy in one and increasing it in the other.

This stimulated much debate among physicists. Leo Szilard in 1929 published a refutation of this by saying that the “Demon” had to process information to make this decision and that processing activity consumed additional energy. He also postulated that the energy requirements for processing the information always exceeded the energy stored through the Demon's sorting.

As a result, when Shannon developed his model of information theory he required all information to be transported along a physical channel. This channel represented the “cost” of transmission specified by Szilard. He was then able to equate the entropy of physical energy with a certain amount of information, called negentropy [6] since it reduced entropy as the Demon does in Figure 1.2.

We can use the metaphor of Maxwell's Demon as a way to interpret the basic problem‐solving process carried out by Cultural Algorithms when successful. We will call this process the Cultural Engine. Recall that the communication protocol for Cultural Algorithms consists of three phases: vote, inherit, and promote (VIP). The voting process is carried out by the acceptance function. The inherit process is carried out by the update function. The promote function is carried out through the influence function. These functions provide the interface between the Population component and the Belief component. Together, similar to Maxwell’s Demon, they extract high entropy individuals first from the population space, update the Belief Space, and then extract high entropy Knowledge Sources from the Belief Space back to modify the Population Space like a two‐stroke thermodynamic engine.