Franco Taroni - Statistics and the Evaluation of Evidence for Forensic Scientists
Здесь есть возможность читать онлайн «Franco Taroni - Statistics and the Evaluation of Evidence for Forensic Scientists» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Statistics and the Evaluation of Evidence for Forensic Scientists
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Statistics and the Evaluation of Evidence for Forensic Scientists: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Statistics and the Evaluation of Evidence for Forensic Scientists»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
he leading resource in the statistical evaluation and interpretation of forensic evidence
The third edition of
is fully updated to provide the latest research and developments in the use of statistical techniques to evaluate and interpret evidence. Courts are increasingly aware of the importance of proper evidence assessment when there is an element of uncertainty. Because of the increasing availability of data, the role of statistical and probabilistic reasoning is gaining a higher profile in criminal cases. That’s why lawyers, forensic scientists, graduate students, and researchers will find this book an essential resource, one which explores how forensic evidence can be evaluated and interpreted statistically. It’s written as an accessible source of information for all those with an interest in the evaluation and interpretation of forensic scientific evidence.
Discusses the entire chain of reasoning–from evidence pre-assessment to court presentation; Includes material for the understanding of evidence interpretation for single and multiple trace evidence; Provides real examples and data for improved understanding. Since the first edition of this book was published in 1995, this respected series has remained a leading resource in the statistical evaluation of forensic evidence. It shares knowledge from authors in the fields of statistics and forensic science who are international experts in the area of evidence evaluation and interpretation. This book helps people to deal with uncertainty related to scientific evidence and propositions. It introduces a method of reasoning that shows how to update beliefs coherently and to act rationally. In this edition, readers can find new information on the topics of elicitation, subjective probabilities, decision analysis, and cognitive bias, all discussed in a Bayesian framework.

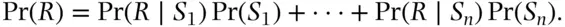
 (Rh
(Rh  ) and
) and  (Rh+) for the father, so here
(Rh+) for the father, so here  . Assume the relative frequencies of the two groups are
. Assume the relative frequencies of the two groups are 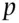 and
and 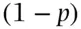 , respectively. The child is Rh
, respectively. The child is Rh  (event
(event 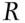 ) and the mother is also Rh
) and the mother is also Rh  (event
(event 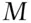 ). The probability of interest is the probability a Rh
). The probability of interest is the probability a Rh  mother will have a Rh
mother will have a Rh  child, in symbols
child, in symbols 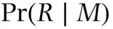 . This probability is not easily derived directly but the derivation is fairly straightforward if the law of total probability is invoked to include the father.
. This probability is not easily derived directly but the derivation is fairly straightforward if the law of total probability is invoked to include the father.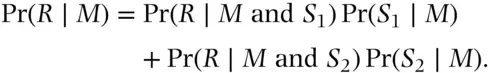
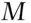 . If both parents are Rh
. If both parents are Rh  , event (
, event (  and
and 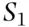 ), then the child is Rh
), then the child is Rh  with probability 1, so
with probability 1, so 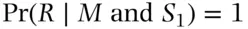 . If the father is Rh+ (the mother is still Rh
. If the father is Rh+ (the mother is still Rh  ), event
), event 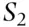 , then
, then 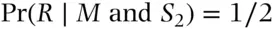 . Assume that parents mate at random with respect to the Rhesus quality. Then
. Assume that parents mate at random with respect to the Rhesus quality. Then 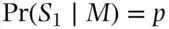 , the relative frequency of Rh
, the relative frequency of Rh  in the population, independent of
in the population, independent of 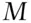 . Similarly,
. Similarly, 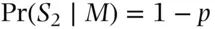 , the relative frequency of Rh+ in the population. These probabilities can now be inserted in ( 1.13) to obtain
, the relative frequency of Rh+ in the population. These probabilities can now be inserted in ( 1.13) to obtain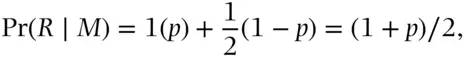
 mother will have a Rh
mother will have a Rh  child. This result is not intuitively obvious, unless one considers the approach based on the law of total probability.
child. This result is not intuitively obvious, unless one considers the approach based on the law of total probability. (event
(event 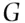 ) in a crime sample for a Caucasian, Maori, or Pacific Islander are 0.012, 0.045, and 0.039, respectively. These values are the assessments for the following three conditional probabilities:
) in a crime sample for a Caucasian, Maori, or Pacific Islander are 0.012, 0.045, and 0.039, respectively. These values are the assessments for the following three conditional probabilities: 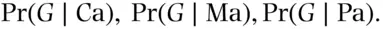 Then the probability of finding the YNH24 genotype,
Then the probability of finding the YNH24 genotype,  , in a person taken at random from the whole population of New Zealand is
, in a person taken at random from the whole population of New Zealand is
 and
and 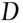 be two genetic marker systems with realisations
be two genetic marker systems with realisations 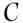 and
and 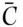 ,
, 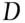 , and
, and 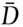 . Let
. Let 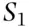 and
and 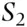 be two mutually exclusive and exhaustive subpopulations such that a person from the population belongs to one and only one of
be two mutually exclusive and exhaustive subpopulations such that a person from the population belongs to one and only one of 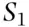 and
and 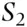 . Let
. Let 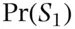 and
and 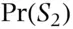 be the probabilities that a person chosen at random from the population belongs to
be the probabilities that a person chosen at random from the population belongs to 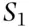 and to
and to 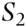 , respectively. Then
, respectively. Then 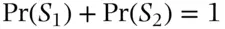 . Within each subpopulation
. Within each subpopulation 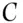 and
and 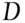 are independent so that the probability an individual chosen at random from one of these subpopulations is of type
are independent so that the probability an individual chosen at random from one of these subpopulations is of type 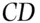 is simply the product of the individual probabilities. Thus
is simply the product of the individual probabilities. Thus










