There is nothing wrong with the frequency interpretation or chance. It has not been used in this treatment because it is often useless. What is the chance that the defendant is guilty? Are we to imagine a sequence of trials in which the judgements, ‘guilty’ or ‘not guilty’, are made and the frequency of the former found? It will not work because it confuses the judgement of guilt, but, more importantly, because it is impossible to conceive of a suitable sequence. Do we repeat the same trial with a different jury; or with the same jury bur different lawyers; or do we take all Scottish trials; or only Scottish trials for the same offence? The whole idea of chance is preposterous in this context. (p. 48)
The example makes clear that a definition of probability based on the long‐run relative frequency of an event is inapplicable in many situations arising in real life. There are implicit assumptions that must apply in each of the classical and frequentist definitions. These assumptions are, first, that according to our state of knowledge, all cases are equally likely, and, second, that it is theoretically possible to perform an experiment a large number of times under identical conditions. Use of these assumptions to assign a numerical value to a probability implies a judgement that these assumptions are satisfied. A definition of probability that seeks to avoid subjectivity is based on an acceptance of assumptions that are inherently subjective. The frequentist view presumes the possibility of the performance of a long sequence of experiments under identical conditions, with each experiment being physically independent of all other experiments. These assumptions are typically unachievable in many different applied contexts such as history, law, economics, medicine, and, especially, forensic science. In these contexts, the events of interest are usually not the result of repetitive or replicable processes. On the contrary, they are unique.
This aspect has been explicitly underlined by Kingston and Kirk (1964) in the area of forensic science. The authors wrote:
There are many philosophically oriented fundamental ideas of probability. Perhaps the most practical basic approach to the subject lies in the concept of frequency, in which statements of probability express the relative frequencies of repeated events. [  ] For practical use in criminalistics, it is of little interest what might happen in a long series of trials; the crime is committed only once. Of what use, then, is the above frequency concept? The answer to this lies in another way of looking at probability, which is to consider it as a degree of belief. (p. 514)
] For practical use in criminalistics, it is of little interest what might happen in a long series of trials; the crime is committed only once. Of what use, then, is the above frequency concept? The answer to this lies in another way of looking at probability, which is to consider it as a degree of belief. (p. 514)
Such complications do not arise with the subjective interpretation of probability because that interpretation does not consider probability as a feature of the external world. Instead probability is understood as a notion that describes the relationship between a person (e.g. You, the reader) who makes a statement of uncertainty and the real world to which that statement relates and in which the person acts. With the subjective concept of probability, it is therefore very reasonable to assign a probability to events that are not repeatable, for example, as in a given judicial context. An extended discussion on the limitations of the classical and frequentist definitions of probability can be found in Taroni et al. (2018).
1.7.5 Subjective Definition of Probability
In forensic science, it is often emphasised that there is a real paucity of numerical data, so that the numerical evaluation of evidence ( Section 2.3.1) is sometimes very difficult. Examples of this difficulty are the numerical assessments of parameters such as transfer or persistence probabilities (see Sections 6.2.3 and 6.2.4) or even the relevance of a piece of evidence (see Section 6.3). The Bayesian approach considers probabilities as measures of belief (also called subjective probabilities) since such probabilities may be thought of as measures of one's belief in the occurrence of a particular event. The approach allows scientists to assign their probabilities, not only by certified knowledge and experience, but also by any data relevant for the event of interest, such as knowledge of an event that is often available in terms of a relative frequency. This specific relationship between relative frequency and probability is discussed in Section 1.7.6. Note that frequency is a term that relates to data and probability is a term that relates to personal belief.
Jurists are also interested in probabilistic reasoning using subjective probabilities, notably probabilities related to the credibility of witnesses and the conclusions that might be drawn from their testimony.
Any kind of uncertainty is assessed in the light of the knowledge possessed at the time of the assessment. This idea is not new. The Italian mathematician Bruno de Finetti (de Finetti, 1931a) defined probability – the measure of uncertainty – as a degree of belief, insisting that probability is conditional on the status of information of the subject who assesses it. So, if a given person, 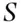 , say, is interested in the probability of an event,
, say, is interested in the probability of an event, 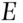 , say, that person's probability
, say, that person's probability 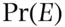 should be written as
should be written as 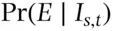 where
where 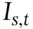 is the information available to person
is the information available to person 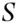 at time
at time 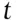 .
.
Subjective probability may be found in many scientific areas (Press and Tanur 2001). In physics, for example, Schrödinger (1947) wrote
Since the knowledge may be different with different persons or with the same person at different times, they may anticipate the same event with more or less confidence and thus different numerical probabilities may be attached to the same event. (p. 53)
He then added that
Thus, whenever we speak loosely of the probability of an event, it is always to be understood: probability with regard to a certain given state of knowledge. (p. 54)
The same perspective is expressed by de Finetti in his famous sentence ‘Probability does not exist’ (in things) (de Finetti 1975, p. x). Probability is not something that can be known or not known, probabilities are states of mind, not states of nature. This aphorism can also be found in previous statistical and philosophical literature (i.e. de Morgan 1838; Jaynes 2003; Jevons 1913; Maxwell 1990). For example, Jevons (1913) wrote
Probability belongs wholly to the mind. This is proved by the fact that different minds may regard the very same event at the same time with widely different degrees of probability [  ,] Probability thus belongs to our mental condition, to the light in which we regard events, the occurrence or non‐occurrence of which is certain in themselves. (p. 198)
,] Probability thus belongs to our mental condition, to the light in which we regard events, the occurrence or non‐occurrence of which is certain in themselves. (p. 198)
Читать дальше

 ] For practical use in criminalistics, it is of little interest what might happen in a long series of trials; the crime is committed only once. Of what use, then, is the above frequency concept? The answer to this lies in another way of looking at probability, which is to consider it as a degree of belief. (p. 514)
] For practical use in criminalistics, it is of little interest what might happen in a long series of trials; the crime is committed only once. Of what use, then, is the above frequency concept? The answer to this lies in another way of looking at probability, which is to consider it as a degree of belief. (p. 514)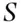 , say, is interested in the probability of an event,
, say, is interested in the probability of an event, 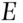 , say, that person's probability
, say, that person's probability 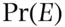 should be written as
should be written as 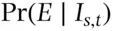 where
where 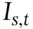 is the information available to person
is the information available to person 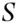 at time
at time 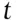 .
. ,] Probability thus belongs to our mental condition, to the light in which we regard events, the occurrence or non‐occurrence of which is certain in themselves. (p. 198)
,] Probability thus belongs to our mental condition, to the light in which we regard events, the occurrence or non‐occurrence of which is certain in themselves. (p. 198)










