Evett (1977) gave an example of the sort of problem that may be considered and developed a procedure for evaluating the evidence that mimicked the interpretative thinking of the forensic scientist of the time. The case is an imaginary one. Five fragments from a suspect are to be compared with 10 fragments from a window broken at the scene of a crime. The values of the refractive index measurements are given in Table 1.2. The procedure developed by Evett is a two‐stage one. It is described here briefly. It is a rather arbitrary and hybrid procedure. While it follows the thinking of the forensic scientist, there are interpretative problems, which are described here, in attempting to provide due value to the evidence. An alternative approach that overcomes these problems is described in Chapter 7.
Table 1.2Refractive index measurements.
| Measurements from the window |
1.518 44 |
1.518 48 |
1.518 44 |
1.518 50 |
1.518 40 |
|
1.518 48 |
1.518 46 |
1.518 46 |
1.518 44 |
1.518 48 |
| Measurements from the PoI |
1.518 48 |
1.518 50 |
1.518 48 |
1.518 44 |
1.518 46 |
The first stage is known as the comparison stage. The two sets of measurements are compared. The comparison takes the form of the calculation of a statistic, 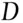 , say. This statistic provides a measure of the difference, known as a standardised difference, between the two sets of measurements that takes account of the natural variation there is in the refractive index measurements of glass fragments from within the same window. If the absolute value of
, say. This statistic provides a measure of the difference, known as a standardised difference, between the two sets of measurements that takes account of the natural variation there is in the refractive index measurements of glass fragments from within the same window. If the absolute value of 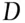 is less than (or equal to) some pre‐specified value, known as a threshold value, then the two sets of fragments are deemed to be similar and the second stage is implemented. If the absolute value of
is less than (or equal to) some pre‐specified value, known as a threshold value, then the two sets of fragments are deemed to be similar and the second stage is implemented. If the absolute value of 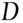 is greater than the threshold value, then the two sets of fragments are deemed to be dissimilar. The two sets of fragments are then deemed to have come from different sources and the second stage is not implemented. (Note the use here of the word statistic , which in this context can be thought of simply as a function of the observations.) A classic example of such an approach is the use of the Student
is greater than the threshold value, then the two sets of fragments are deemed to be dissimilar. The two sets of fragments are then deemed to have come from different sources and the second stage is not implemented. (Note the use here of the word statistic , which in this context can be thought of simply as a function of the observations.) A classic example of such an approach is the use of the Student 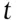 ‐test or the modified Welch test for the comparison of means (Welch 1937; Walsh et al. 1996; Curran et al. 2000).
‐test or the modified Welch test for the comparison of means (Welch 1937; Walsh et al. 1996; Curran et al. 2000).
The second stage is known as the significance stage. This stage attempts to determine the significance of the finding from the first stage that the two sets of fragments were similar. The significance is determined by calculating the probability of the result that the two sets of fragments were found to be similar, under the assumption that the two sets had come from different sources. If this probability is very low then this assumption is deemed to be false. The fragments are then assumed to come from the same source, an assumption that places the PoI at the crime scene. This assumption says nothing about how the fragments came to be associated with the PoI. This may have occurred in an innocent manner. See Section 5.3.2 for further discussion of this point in the context of activity level propositions.
The procedure can be criticised on two points. First, in the comparison stage the threshold provides a qualitative step that may provide very different outcomes for two different pairs of observations. One pair of sets of fragments may provide a value of 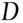 , which is just below the threshold, whereas the other pair may provide a value of
, which is just below the threshold, whereas the other pair may provide a value of 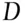 just above the threshold. The first pair will proceed to the significance stage, the second stage will not. Yet, the two pairs may have measurements, which are close together. The difference in the consequences is greater than the difference in the measurements merits (such an approach is called a fall‐off‐the‐cliff effect; see Evett (1991) who attributed this term to Ken Smalldon. Criticisms have been developed in Robertson and Vignaux (1995b). They wrote:
just above the threshold. The first pair will proceed to the significance stage, the second stage will not. Yet, the two pairs may have measurements, which are close together. The difference in the consequences is greater than the difference in the measurements merits (such an approach is called a fall‐off‐the‐cliff effect; see Evett (1991) who attributed this term to Ken Smalldon. Criticisms have been developed in Robertson and Vignaux (1995b). They wrote:
This sudden change in decision due to crossing a particular line is likened to falling off a cliff, one moment you are safe, the next dead. In fact, rather than a cliff we have merely a steep slope. Other things being equal, the more similar the samples the stronger the evidence that they had a common origin, and the less similar the samples the stronger the evidence that they came from different sources. (p. 118)
A related problem is that of cut‐off where a decision is taken dependent on whether a statistic is above or below a certain value (see Section 7.7.5).
A better approach, as suggested in the quotation from Robertson and Vignaux (1995b) above and that is described in Section 7.3, provides a measure of the value of the evidence that decreases as the distance between the two sets of measurements increases, subject, as explained later, to the rarity or otherwise of the measurements.
The second criticism is that the result is difficult to interpret. Because of the effect of the comparison stage, the result is not just simply the probability of the evidence, assuming the two sets of fragments came from different sources. A reasonable interpretation, as will be explained in Section 2.4, of the value of the evidence is the effect that it has on the odds in favour of the true guilt of the PoI. In the two‐stage approach this effect is difficult to measure. The first stage discards certain sets of measurements, which may have come from the same source and does not discard other sets of measurements which may have come from different sources. The second stage calculates a probability, not of the evidence but of that part of the evidence for which 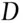 was not greater than the threshold value, assuming the two sets came from different sources. It is necessary, as is seen later, to compare this probability with the probability of the same result, assuming the two sets came from the same source. There is also an implication in the determination of the probability in the significance stage that a small probability for the evidence, assuming the two sets came from different sources, means that there is a large probability that the two sets came from the same source. This implication is unfounded; see Section 2.5.1.
was not greater than the threshold value, assuming the two sets came from different sources. It is necessary, as is seen later, to compare this probability with the probability of the same result, assuming the two sets came from the same source. There is also an implication in the determination of the probability in the significance stage that a small probability for the evidence, assuming the two sets came from different sources, means that there is a large probability that the two sets came from the same source. This implication is unfounded; see Section 2.5.1.
A review of the two‐stage approach and the development of a Bayesian approach is provided by Curran et al. (2000) and Curran and Hicks (2009).
As with DNA profiling, there are problems associated with the definition of a suitable population from which probability distributions for refractive measurements may be obtained; see, for example, Walsh and Buckleton (1986).
These examples have been introduced to provide a framework within which the evaluation of evidence may be considered. In order to evaluate evidence, something about which there is much uncertainty, it is necessary to establish a suitable terminology and to have some method for the assessment of uncertainty. First, some terminology will be introduced followed by a method for the measurement of uncertainty. This method is probability . The role of uncertainty, as represented by probability, in the assessment of the value of scientific evidence will form the basis of the rest of this chapter. A commentary on so‐called knowledge management , of which this is one part, has been given by Evett (1993b, 2015).
Читать дальше

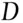 , say. This statistic provides a measure of the difference, known as a standardised difference, between the two sets of measurements that takes account of the natural variation there is in the refractive index measurements of glass fragments from within the same window. If the absolute value of
, say. This statistic provides a measure of the difference, known as a standardised difference, between the two sets of measurements that takes account of the natural variation there is in the refractive index measurements of glass fragments from within the same window. If the absolute value of 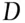 is less than (or equal to) some pre‐specified value, known as a threshold value, then the two sets of fragments are deemed to be similar and the second stage is implemented. If the absolute value of
is less than (or equal to) some pre‐specified value, known as a threshold value, then the two sets of fragments are deemed to be similar and the second stage is implemented. If the absolute value of 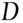 is greater than the threshold value, then the two sets of fragments are deemed to be dissimilar. The two sets of fragments are then deemed to have come from different sources and the second stage is not implemented. (Note the use here of the word statistic , which in this context can be thought of simply as a function of the observations.) A classic example of such an approach is the use of the Student
is greater than the threshold value, then the two sets of fragments are deemed to be dissimilar. The two sets of fragments are then deemed to have come from different sources and the second stage is not implemented. (Note the use here of the word statistic , which in this context can be thought of simply as a function of the observations.) A classic example of such an approach is the use of the Student 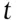 ‐test or the modified Welch test for the comparison of means (Welch 1937; Walsh et al. 1996; Curran et al. 2000).
‐test or the modified Welch test for the comparison of means (Welch 1937; Walsh et al. 1996; Curran et al. 2000).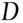 , which is just below the threshold, whereas the other pair may provide a value of
, which is just below the threshold, whereas the other pair may provide a value of 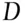 just above the threshold. The first pair will proceed to the significance stage, the second stage will not. Yet, the two pairs may have measurements, which are close together. The difference in the consequences is greater than the difference in the measurements merits (such an approach is called a fall‐off‐the‐cliff effect; see Evett (1991) who attributed this term to Ken Smalldon. Criticisms have been developed in Robertson and Vignaux (1995b). They wrote:
just above the threshold. The first pair will proceed to the significance stage, the second stage will not. Yet, the two pairs may have measurements, which are close together. The difference in the consequences is greater than the difference in the measurements merits (such an approach is called a fall‐off‐the‐cliff effect; see Evett (1991) who attributed this term to Ken Smalldon. Criticisms have been developed in Robertson and Vignaux (1995b). They wrote: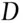 was not greater than the threshold value, assuming the two sets came from different sources. It is necessary, as is seen later, to compare this probability with the probability of the same result, assuming the two sets came from the same source. There is also an implication in the determination of the probability in the significance stage that a small probability for the evidence, assuming the two sets came from different sources, means that there is a large probability that the two sets came from the same source. This implication is unfounded; see Section 2.5.1.
was not greater than the threshold value, assuming the two sets came from different sources. It is necessary, as is seen later, to compare this probability with the probability of the same result, assuming the two sets came from the same source. There is also an implication in the determination of the probability in the significance stage that a small probability for the evidence, assuming the two sets came from different sources, means that there is a large probability that the two sets came from the same source. This implication is unfounded; see Section 2.5.1.










