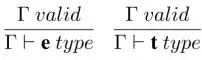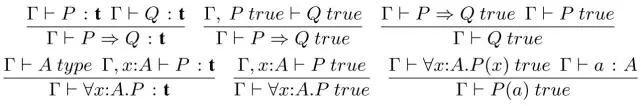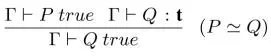In MTTs, the correctness of typing judgments of the form a : A , stating that a is of type A , is decidable in the sense that we can mechanically decide whether such a judgment can be correctly made. For computer scientists, this is equivalent to saying that a computer system can automatically decide whether a is of type A. Thanks to this decidability result and because of the rich typing mechanisms in MTTs, the Curry–Howard principle of propositions-as-types (Curry and Feys 1958; Howard 1980) gives us an embedded logical mechanism for semantic interpretations – the second requirement above. In this book, we shall elaborate this in detail to illustrate how the logical mechanisms work and how the typing mechanisms facilitate semantic formalizations.
MTTs are specified by means of proof-theoretic rules (see Chapter 2) and, because of this, there are two advantageous facets that are not available in previous set-theoretic semantics: the first is that an MTT can have a use theory of meaning in that its judgments (sentences) can be understood proof-theoretically by means of their inferential uses. Such a proof-theoretic understanding of a foundational semantic language was not available before: we cannot understand set theory in such a way. Therefore, this offers us a new possibility: we may claim that an MTT, as the foundational semantic language, is well understood by means of its proof-theoretic meaning theory. Second, because they are proof-theoretically specified, MTTs (and hence MTT-semantics) can be readily implemented on computers to support computer-assisted reasoning in natural language. In fact, this is supported by the current proof technology provided by the proof assistants based on MTTs, as mentioned above, and we shall describe how MTT-semantics can be implemented on computers to perform reasoning tasks in natural language.
1.3. Montague’s model-theoretic semantics
Since its development in the late 1960s and early 1970s, Montague semantics (Montague 1974) has been the dominant approach to formal semantics. There are several textbooks about Montague semantics including, for example, that by Dowty et al . (1981). As explained above, Montague has introduced an intermediate language, called Intensional Logic (IL), for his model-theoretic semantics. For instance, to interpret the sentence in ( 1.1), we could first give its interpretation ( 1.2) in IL, where the semantics of John is an entity j and the semantic interpretation talk of the verb “talk” is a predicate over entities of the world, which can be applied to j to form the interpretation ( 1.2):
( 1.1) John talks.
( 1.2) talk(j)
This then gives the set-theoretical interpretation of ( 1.1), i.e. the interpretation of ( 1.2) in set theory (according to, for example, Henkin’s model interpretation), which says that the set-theoretic interpretation of j is a member of the set that interprets the predicate talk .
In what follows, we shall first describe simple type theory 6 and then how it is used in Montague semantics.
1.3.1. Simple type theory: a formal description
Montague’s IL (Montague 1973; Gallin 1975) consists of an extensional core, which is Church’s simple type theory (Church 1940) (we call it C in this book, with C standing for “Church”), and a part concerning intensionality. 7 We shall focus on describing the former and then briefly comment on the part about intensionality.
Our description of Church’s simple type theory C follows that by Luo and Soloviev (2017), where it is described by means of natural deduction rules that derive judgments – sentences in the type theory. For instance, a judgment may be of the form Γ ├ a : A , which means that a is of type A under the assumptions described in context Γ. We shall first explain what contexts and judgments are in C , and then describe its rules. 8 (All of C ’s inference rules are listed in Appendix A1.1.)
Contexts and Judgments. A context is a sequence of entries either of the form x : A or of the form P true . Informally, the former assumes that the variable x be of type A and the latter that the proposition P be true. Only valid contexts are legal and context validity is governed by the following rules:
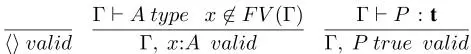
where 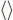 is the empty sequence and FV (Γ) is the set of free variables in Γ, defined as: (1) FV (
is the empty sequence and FV (Γ) is the set of free variables in Γ, defined as: (1) FV (  ) = ∅; (2) FV (Γ, x:A ) = FV (Γ) ∪{ x }; (3) FV (Γ, P true ) = FV (Γ).
) = ∅; (2) FV (Γ, x:A ) = FV (Γ) ∪{ x }; (3) FV (Γ, P true ) = FV (Γ).
Judgments are sentences of C , whose correctness is governed by the inference rules below. In C , there are four forms of judgments:
– Γ valid, which means that Γ is a valid context (the rules of deriving context validity are given above);
– Γ ├ A type, which means that A is a type under context Γ;
– Γ ├ a : A, which means that a is an object of type A under context Γ;
– Γ ├ P true, which means that P is a true formula under context Γ.
Inference rules . Besides the context validity rules given above, C has the following rules:
– Rules for base types: eand tare the types of entities and logical formulae, respectively. 9
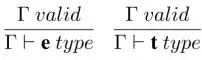
– Assumption rules: one can prove what have been assumed in valid contexts.
– Rules for function types: The formation rule (of function types), introduction rule (of λ-abstraction) and elimination rule (for applications) are as follows, where the terms in the forms of λ-abstractions and applications are related to each other computationally by the relation of β-conversion. 10
– Rules for logical formulae formed by implication and universal quantification: their formation, introduction and elimination rules.
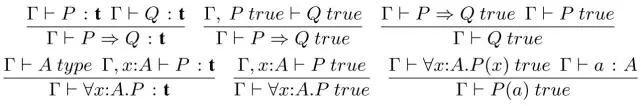
where, in the last rule, P (a) is obtained by substituting a for x in P (x) .
– Conversion rule for truth of formulas (see footnote 10 for the conversion relation ≈):
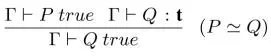
Logical operators . The other usual logical operators can be defined by means of ⇒ and ∀. For example, the operators for conjunction and existential quantification can be defined as follows. Other operators such as disjunction and negation can be defined similarly (see Appendix A1.2).
(1.3) P ∧ Q = ∀X : t. (P ⇒ Q ⇒ X) ⇒ X
(1.4) ∃x : A.P (x) = ∀X : t. (∀x : A.(P (x) ⇒ X)) ⇒ X
Table 1.1. Examples in Montague semantics
|
Example |
Montague semantics |
| CN |
man, human |
man, human : e → t |
| IV |
talk |
talk : e → t |
| ADJ |
handsome |
handsome : (e → t) → (e → t) |
| ADV VP |
quickly |
quickly : (e → t) → (e → t) |
| Modified CN |
handsome man |
handsome(man) : e → t |
| Quantifier |
some |
some : (e → t) → (e → t) → t |
| S |
A man talks |
∃ x : e. man(x) & talk(x) : t |
1.3.2. Montague semantics: examples and intensionality
Читать дальше

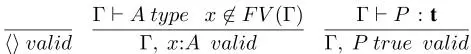
 is the empty sequence and FV (Γ) is the set of free variables in Γ, defined as: (1) FV (
is the empty sequence and FV (Γ) is the set of free variables in Γ, defined as: (1) FV (