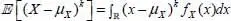Probability theory is the most widely used approach for the representation of uncertainties. Its theoretical framework is recalled here from an angle that makes it easy to compare it subsequently with alternative uncertainty representation approaches. We shall also present some situations illustrating the limits of probability theory for representing some types of epistemic uncertainties.
1.3.1. Theoretical context
Formally, probabilities are defined on a probability space EP defined as follows.
DEFINITION 1.1.– Let Ω be a set. A σ- algebra or σ- field on Ω refers to a set T of subsets of Ω verifying:
– T not empty: T ≠ ∅;
– T stable by complementary: ∀A ∈ T, AC ∈ T;
– T stable by countable union: .
DEFINITION 1.2.– Let Ω be a set and T a σ- algebra of Ω. A probability measure on (Ω, T) is a function ℙ : T → ℝ satisfying the following three axioms, called Kolmogorov axioms:
– the function has values between 0 and 1: ∀A ∈ T,0 ≤ ℙ (A) ≤ 1;
– the image of all the events in the universe is 1: ℙ (Ω) = 1;
– the function is σ-additive: .
DEFINITION 1.3.– Let Ω be a set, T a σ-algebra of Ω and ℙ a probability measure. The triplet ( Ω, T, ℙ) is called a probability space EP .
Concretely, Ω is called a universe, comprising the set of the possible events (or outcomes) under consideration. T is a subset of the universe, that is, a subset of possible events, having a σ-algebra structure. ℙ is a probability measure that allows a certain probability to be attributed to any event in the universe.
PROPERTY 1.1.– Let (Ω, T , ℙ ) denote a probability space. Then ∀ A ∈ T , ℙ ( A ) + ℙ ( AC ) = 1.
This property is trivial within the context of probability theory, but we shall see that in alternative theories of representation of uncertainties it appears differently.
DEFINITION 1.4.– Let ( Ω, T, ℙ) be a probability space. Any measurable function from Ω to ℝ is called a real-valued random variable X. x = X(ω) is called a realization of the random variable X:
[1.1] 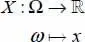
DEFINITION 1.5.– The probability distribution of the real-valued random variable X is the probability measure, denoted ℙ X , resulting from the transport of the probability measure ℙ on Ω into a probability measure ℙX on ℝ .
The probability distribution ℙX is then a function that allows any subset of ℝ to be associated with an associated probability. Note that there are different types of probability distributions, some examples of which are the binomial, geometric or Bernoulli distributions for discrete random variables and normal (or Gaussian), uniform or gamma distributions for continuous random variables. In the following, we will be interested, essentially, in continuous random variables, which are those most often used in engineering problems.
DEFINITION 1.6.– The cumulative distribution function (CDF), sometimes referred to as the distribution function (DF), of the probability distribution ℙX is the function FX defined by:
[1.2] 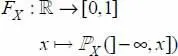
The CDF thus associates to any real value x the value of the probability that the random variable of distribution ℙX is less than or equal to the value x .
DEFINITION 1.7.– The complementary cumulative distribution function (CCDF), sometimes called the complementary cumulative probability function (CCPF), of the probability distribution ℙX is the function defined by:
[1.3] 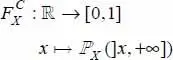
The CCDF is introduced here because it is sometimes used in risk analysis, where it provides a means to know what is the probability that a quantity will exceed a threshold.
An example of CDF and CCDF is provided in Figure 1.1for a Gaussian distribution of mean 4 and standard deviation 1.
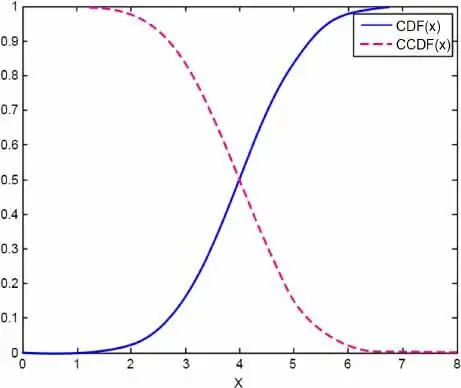
Figure 1.1. Example of a cumulative distribution function (CDF) and a complementary cumulative distribution function (CCDF) corresponding to a Gaussian probability distribution of mean 4 and standard deviation 1. For a color version of this figure, see www.iste.co.uk/gogu/uncertainties.zip
DEFINITION 1.8.– For a random variable of absolutely continuous distribution (by misuse of language, this is referred to as continuous random variable), the probability density function (PDF) is defined by
[1.4] 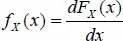
DEFINITION 1.9.– The expectation of a real-valued continuous random variable is given as
[1.5] 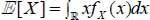
The expectation of a random variable corresponds to the mean expected value or, by misuse of language, the mean value. It is often denoted as μX .
DEFINITION 1.10.– The variance of a real-valued continuous random variable is given as
[1.6] 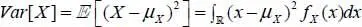
The variance corresponds to the dispersion of the values of the variable around its mean value. It is often denoted 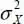 and its square root σX is called the standard deviation. The coefficient of variation ( CoV ) of the random variable is then defined by
and its square root σX is called the standard deviation. The coefficient of variation ( CoV ) of the random variable is then defined by 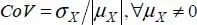 .
.
DEFINITION 1.11.– The k-order centered moment of a real-valued continuous random variable is written as
[1.7] 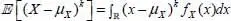
Note that the second-order centered moment is the variance. The third-order centered moment is usually referred to as the coefficient of skewness, and characterizes the asymmetry of the probability distribution of the random variable. The fourth-order centered moment is usually referred to as kurtosis and characterizes the flattening of the probability distribution of the random variable.
Читать дальше

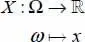
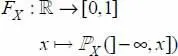
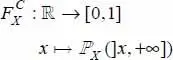

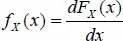
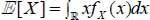
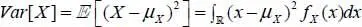
 and its square root σX is called the standard deviation. The coefficient of variation ( CoV ) of the random variable is then defined by
and its square root σX is called the standard deviation. The coefficient of variation ( CoV ) of the random variable is then defined by 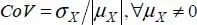 .
.