EXAMPLE 2.2.– Let us evaluate the expression ! x + y
in the state 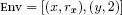 and
and 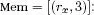
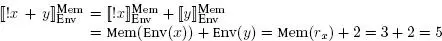
The evaluation function 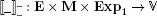 is obtained directly as follows:
is obtained directly as follows:
Python def eval_exp1(env,mem,e): if isinstance(e,Cste1): return VCste1(CInt1(e.cste)) if isinstance(e,Var1): x = valeur_de(env,e.symb) if isinstance(x,CInt1) or isinstance(x,CRef1): return VCste1(x) return Erreur1() if isinstance(e,Plus1): ev1 = eval_exp1(env,mem,e.exp1) if isinstance(ev1,Erreur1): return Erreur1() v1 = ev1.cste ev2 = eval_exp1(env,mem,e.exp2) if isinstance(ev2,Erreur1): return Erreur1() v2 = ev2.cste if isinstance(v1,CInt1) and isinstance(v2,CInt1): return VCste1(CInt1(v1.cst_int + v2.cst_int)) return Erreur1() if isinstance(e,Bang1): x = valeur_de(env,e.symb) if isinstance(x,CRef1): y = valeur_ref(mem,x.cst_adr) if y is None: return Erreur1() return VCste1(y) return Erreur1() raise ValueErrorOCaml let rec eval_exp1 env mem e = match e with | Cste1 n -> VCste1 (CInt1 n) | Var1 x -> (match valeur_de env x with Some v -> VCste1 v | _ -> Erreur1) | Plus1 (e1, e2) -> ( match ((eval_exp1 env mem e1), (eval_exp1 env mem e2)) with | (VCste1 (CInt1 n1), VCste1 (CInt1 n2)) -> VCste1 (CInt1 (n1 + n2)) | _ -> Erreur1) | Bang1 x -> (match valeur_de env x with | Some (CRef1 a) -> (match valeur_ref mem a with Some v -> VCste1 v | _ -> Erreur1) | _ -> Erreur1) val eval_exp1 : (’a * ’b const1) list -> (’b * ’b const1) list -> ’a exp1 -> ’b valeurs1
Considering example 2.2, we obtain:
Python ex_env1 = [(“x”,CRef1(“rx”)),(“y”,CInt1(2))] ex_mem1 = [(“rx”,CInt1(3))] >>> (eval_exp1(ex_env1,ex_mem1,ex_exp1)).cste.cst_int 5OCaml let ex_env1 = [ (“x”, CRefl (“rx”)); (“y”, CIntl (2)) ] val ex_env1 : (string * string constl) list let ex_mem1 = [ (“rx”, CIntl (3)) ] val ex_mem1 : (string * ‘a constl) list # (eval_exp1 ex_env1 ex_mem1 ex_exp1) ;; - : string valeursl = VCstel (CIntl 5)
2.3. Definition and assignment
2.3.1. Defining an identifier
The language Def 1extends Exp 1by adding definitions of identifiers. There are two constructs that make it possible to introduce an identifier naming a mutable or non-mutable variable (as defined in section 2.1.3). Note that, in both cases, the initial value must be provided. This value corresponds to a constant or to the result of a computation specified by an expression e ∈ Exp 1. These constructs modify the current state of the system; after computing 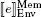 , the next step in evaluating let x = e ; is to add the binding ( x ,
, the next step in evaluating let x = e ; is to add the binding ( x , 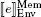 ) to the environment, while the evaluation of var x = e ; adds a binding ( x , r x) to the environment and writes the value
) to the environment, while the evaluation of var x = e ; adds a binding ( x , r x) to the environment and writes the value 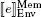 to the reference rx . In this case, we assume that the location denoted by the reference rx is computed by an external mechanism responsible for memory allocation.
to the reference rx . In this case, we assume that the location denoted by the reference rx is computed by an external mechanism responsible for memory allocation.
Table 2.3. Language Def1 of definitions
| d ::= let x = e ; |
Definition of a non-mutable variable |
( x ∈ X, e ∈ Exp 1) |
| | var x = e ; |
Definition of a mutable variable |
( x ∈ X, e ∈ Exp 1) |
The evaluation of a definition is expressed as follows:
(2.1) 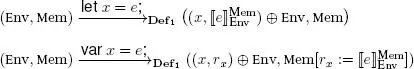
This evaluation → Def 1defines a relation between a state, a definition and a resulting state, or, in formal terms:
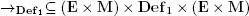
Starting with a finite sequence of definitions d= [ d 1; . . . d n] and an initial state (Env 0, Mem 0), this relation produces the state (Env n, Mem n):
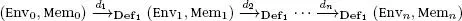
This sequence of transitions may, more simply, be noted 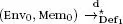 (Env n, Mem n).
(Env n, Mem n).
EXAMPLE 2.3.– Starting with a memory with no accessible references and an “empty” environment, the sequence [var y = 2; let x = ! y + 3;] builds the following state:
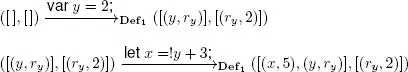
In the environment Env = [( x , 5), ( y , ry )], we obtain 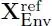 = { y } and
= { y } and  = { x }.
= { x }.
NOTE.– In the definition of the two transitions in [2.1], we presume that the result of the evaluation of the expression e , denoted as 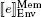 , is not an error result. In the case of an error, no state will be produced and the evaluation stops.
, is not an error result. In the case of an error, no state will be produced and the evaluation stops.
The abstract syntax of language Def 1may be defined as follows:
Python class Let_def1: def __init__(self,var,exp): self.var = var self.exp = exp class Var_def1: def __init__(self,var,exp): self.var = var self.exp = exp OCaml type ’a defl = Let_def1 of ’a * ’a expl | Var_def1 of ’a * ’a expl
We choose to construct a value corresponding to a reference using a constructor applied to an identifier.
Python class Ref_Var1: def __init__(self,idvar): self.idvar = idvarOCaml type ’a refer = Ref_Var1 of ’a
Hence, rx will be represented by Ref_Var1(”x”). As the relation →Def 1defines a function, it can be implemented directly as follows:
Python def trans_def1(st,d): (env,mem) = st if isinstance(d,Let_def1): v = eval_exp1(env,mem,d.exp) if isinstance(v,VCste1): return (ajout_liaison_env(env,d.var,v.cste),mem) raise ValueError if isinstance(d,Var_def1): v = eval_exp1(env,mem,d.exp) if isinstance(v,VCste1): r = Ref_Var1(d.var) return (ajout_liaison_env(env,d.var,CRef1(r)), write_mem(mem,r,v.cste)) raise ValueError raise ValueErrorOCaml let trans_def1 (env, mem) d = match d with | Let_def1 (x, e) -> (match eval_exp1 env mem e with | VCste1 v -> ((ajout_liaison_env env x v), mem) | Erreur1 -> failwith “Erreur”) | Var_def1 (x, e) -> (match eval_exp1 env mem e with | VCste1 v -> ((ajout_liaison_env env x (CRef1 (Ref_Var1 x))), (write_mem mem (Ref_Var1 x) v)) | Erreur1 -> failwith “Erreur”) val trans_def1 : (’a * ’a refer const1) list * (’a refer * ’a refer const1) list -> ’a def1 -> (’a * ’a refer const1) list * (’a refer * ’a refer const1) list
Читать дальше

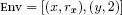 and
and 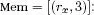
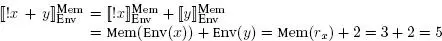
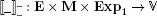 is obtained directly as follows:
is obtained directly as follows: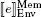 , the next step in evaluating let x = e ; is to add the binding ( x ,
, the next step in evaluating let x = e ; is to add the binding ( x , 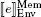 ) to the environment, while the evaluation of var x = e ; adds a binding ( x , r x) to the environment and writes the value
) to the environment, while the evaluation of var x = e ; adds a binding ( x , r x) to the environment and writes the value 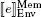 to the reference rx . In this case, we assume that the location denoted by the reference rx is computed by an external mechanism responsible for memory allocation.
to the reference rx . In this case, we assume that the location denoted by the reference rx is computed by an external mechanism responsible for memory allocation.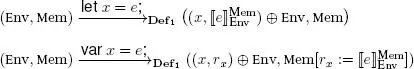
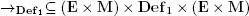
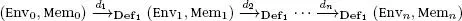
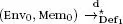 (Env n, Mem n).
(Env n, Mem n).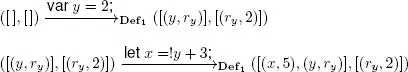
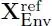 = { y } and
= { y } and  = { x }.
= { x }.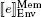 , is not an error result. In the case of an error, no state will be produced and the evaluation stops.
, is not an error result. In the case of an error, no state will be produced and the evaluation stops.










