Gradually, the magnetic vector potential became the problem‐solving tool if not the physical reality. Further, by using the retarded scalar and vector potentials and Lorentz gauge condition 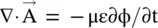 connecting both the vector and scalar potentials, Lorentz formulated the EM‐theory of Maxwell in terms of the magnetic vector potential. In his formulation, a current is the source of the magnetic vector potential
connecting both the vector and scalar potentials, Lorentz formulated the EM‐theory of Maxwell in terms of the magnetic vector potential. In his formulation, a current is the source of the magnetic vector potential  . So, Lorentz considered the propagation of both the magnetic vector and electric scalar potential with a finite velocity that resulted in the retarded time at the field point. However, Maxwell's scalar potential was nonpropagating. Maxwell did not write a wave equation for the scalar potential, as his use of Coulomb gauge
. So, Lorentz considered the propagation of both the magnetic vector and electric scalar potential with a finite velocity that resulted in the retarded time at the field point. However, Maxwell's scalar potential was nonpropagating. Maxwell did not write a wave equation for the scalar potential, as his use of Coulomb gauge 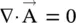 was inconsistent with it. Later on, even electric vector potential
was inconsistent with it. Later on, even electric vector potential  was introduced in the formulation of EM‐theory. The nonphysical magnetic current, introduced in Maxwell's equations by Heaviside, is the source of potential
was introduced in the formulation of EM‐theory. The nonphysical magnetic current, introduced in Maxwell's equations by Heaviside, is the source of potential  . The use of vector potentials simplified the computation of the fields due to radiation from wire antenna and aperture antenna. A component of the magnetic/electric vector potential is a scalar quantity. It has further helped the reformulation of EM‐field theory in terms of the electric scalar and magnetic scalar potentials [B.9, B.10]. Such formulations are used in the guided‐waves analysis. In recent years, it has been pointed out that the Lorentz gauge condition and retarded potentials were formulated by Lorenz in 1867, much before the formulation of famous H. A. Lorentz [J.14, J.15]. However, most of the textbooks refer to the name of Lorentz.
. The use of vector potentials simplified the computation of the fields due to radiation from wire antenna and aperture antenna. A component of the magnetic/electric vector potential is a scalar quantity. It has further helped the reformulation of EM‐field theory in terms of the electric scalar and magnetic scalar potentials [B.9, B.10]. Such formulations are used in the guided‐waves analysis. In recent years, it has been pointed out that the Lorentz gauge condition and retarded potentials were formulated by Lorenz in 1867, much before the formulation of famous H. A. Lorentz [J.14, J.15]. However, most of the textbooks refer to the name of Lorentz.
Both Heaviside and Hertz considered only the electric and magnetic fields as real physical quantities, and magnetic vector and electric scalar potentials as merely auxiliary nonphysical mathematical concepts to solve the EM‐field problem. Possibly, this was not the attitude of Kelvin and Maxwell. They identified the electrical potential with energy, and magnetic vector potential with momentum. The magnetic vector potential  could be considered as the potential momentum per unit charge , just as the electric scalar potential ϕ is the potential energy per unit charge [J.16]. The potential momentum
could be considered as the potential momentum per unit charge , just as the electric scalar potential ϕ is the potential energy per unit charge [J.16]. The potential momentum 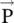 is obtained as follows:
is obtained as follows:
(1.1.2) 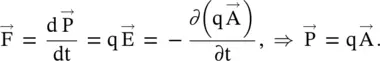
In the above equation, 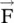 is the force acting on the charge q, and
is the force acting on the charge q, and 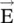 is given by equation ( 1.1.1b).
is given by equation ( 1.1.1b).
Lebedev in 1900 experimentally demonstrated the radiation pressure, demonstrating momentum carried by the EM‐wave. The energy and momentum carried by the EM‐wave indicate that the light radiation could be viewed as some kind of particle, not a wave phenomenon. A particle is characterized by energy and momentum. Such a dual nature of light is a quantum mechanical duality phenomenon. Einstein introduced the concept of the light particle, called “photon” to explain the interaction of light with matter, i.e. the photoelectric effect . However, Lorentz retained the classical wave model to explain the interaction between radiation and matter via polarization of dipoles in a material creating its frequency‐dependent permittivity.
It is to be noted that at a location in the space, even for zero 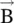 and
and 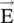 fields, the potentials
fields, the potentials 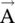 and ϕ could exist [B.11]. Aharonov–Bohm predicted that the potential fields
and ϕ could exist [B.11]. Aharonov–Bohm predicted that the potential fields 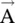 and ϕ, in the absence of
and ϕ, in the absence of 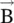 and
and 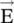 , could influence a charged particle. Tonomura and collaborators experimentally confirmed the validity of Aharonov–Bohm prediction. The Aharonov–Bohm effect demonstrates that
, could influence a charged particle. Tonomura and collaborators experimentally confirmed the validity of Aharonov–Bohm prediction. The Aharonov–Bohm effect demonstrates that 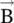 and
and 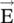 fields only partly describe the EM‐fields in quantum mechanics. The vector potential also has to be retained for a complete description of the EM‐field quantum mechanically [J.3, J.16, J.17]. However, to solve the classical electromagnetic problems, such as guided wave propagation and radiation from antenna, Heaviside formulation of Maxwell equations and potential functions as additional tools is adequate.
fields only partly describe the EM‐fields in quantum mechanics. The vector potential also has to be retained for a complete description of the EM‐field quantum mechanically [J.3, J.16, J.17]. However, to solve the classical electromagnetic problems, such as guided wave propagation and radiation from antenna, Heaviside formulation of Maxwell equations and potential functions as additional tools is adequate.
The above brief review omitted developments in the electromagnetic properties of the material medium. A few important developments could be summarized. In 1837, Faraday introduced the concept of the dielectric constant of a material. In 1838, he introduced the concept of electric polarization 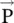 in dielectrics under the influence of the external electric field. Soon after the discovery of the electron in 1897 by J.J. Thomson, the models around electrons were developed to describe the electromagnetic properties of a material. Around 1898, John Gaston Leathem obtained an important relation
in dielectrics under the influence of the external electric field. Soon after the discovery of the electron in 1897 by J.J. Thomson, the models around electrons were developed to describe the electromagnetic properties of a material. Around 1898, John Gaston Leathem obtained an important relation 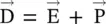 , connecting the displacement of charges in a material with polarization. Kelvin, in the year 1850, developed the concept of magnetic permeability and susceptibility with separate concepts of
, connecting the displacement of charges in a material with polarization. Kelvin, in the year 1850, developed the concept of magnetic permeability and susceptibility with separate concepts of 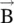 ,
, 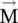 , and
, and  to characterize a magnetic material. In 1900, Drude developed the electrical conduction model, now known as the Drude model , after electron theory. Subsequently, the model was extended to the dielectric medium by Lorentz in 1905. The model called the Drude‐Lorentz model explains the dispersive property of dielectrics. In the year 1912, Debye developed the concept of dipole moment and obtained equations relating it to the dielectric constant. These models laid the foundation to study of the electric and magnetic properties of natural and engineered materials under the influence of external fields [B.4, B.6, B.7, B.12]
to characterize a magnetic material. In 1900, Drude developed the electrical conduction model, now known as the Drude model , after electron theory. Subsequently, the model was extended to the dielectric medium by Lorentz in 1905. The model called the Drude‐Lorentz model explains the dispersive property of dielectrics. In the year 1912, Debye developed the concept of dipole moment and obtained equations relating it to the dielectric constant. These models laid the foundation to study of the electric and magnetic properties of natural and engineered materials under the influence of external fields [B.4, B.6, B.7, B.12]
Читать дальше

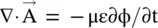 connecting both the vector and scalar potentials, Lorentz formulated the EM‐theory of Maxwell in terms of the magnetic vector potential. In his formulation, a current is the source of the magnetic vector potential
connecting both the vector and scalar potentials, Lorentz formulated the EM‐theory of Maxwell in terms of the magnetic vector potential. In his formulation, a current is the source of the magnetic vector potential  . So, Lorentz considered the propagation of both the magnetic vector and electric scalar potential with a finite velocity that resulted in the retarded time at the field point. However, Maxwell's scalar potential was nonpropagating. Maxwell did not write a wave equation for the scalar potential, as his use of Coulomb gauge
. So, Lorentz considered the propagation of both the magnetic vector and electric scalar potential with a finite velocity that resulted in the retarded time at the field point. However, Maxwell's scalar potential was nonpropagating. Maxwell did not write a wave equation for the scalar potential, as his use of Coulomb gauge 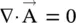 was inconsistent with it. Later on, even electric vector potential
was inconsistent with it. Later on, even electric vector potential 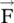 was introduced in the formulation of EM‐theory. The nonphysical magnetic current, introduced in Maxwell's equations by Heaviside, is the source of potential
was introduced in the formulation of EM‐theory. The nonphysical magnetic current, introduced in Maxwell's equations by Heaviside, is the source of potential 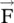 . The use of vector potentials simplified the computation of the fields due to radiation from wire antenna and aperture antenna. A component of the magnetic/electric vector potential is a scalar quantity. It has further helped the reformulation of EM‐field theory in terms of the electric scalar and magnetic scalar potentials [B.9, B.10]. Such formulations are used in the guided‐waves analysis. In recent years, it has been pointed out that the Lorentz gauge condition and retarded potentials were formulated by Lorenz in 1867, much before the formulation of famous H. A. Lorentz [J.14, J.15]. However, most of the textbooks refer to the name of Lorentz.
. The use of vector potentials simplified the computation of the fields due to radiation from wire antenna and aperture antenna. A component of the magnetic/electric vector potential is a scalar quantity. It has further helped the reformulation of EM‐field theory in terms of the electric scalar and magnetic scalar potentials [B.9, B.10]. Such formulations are used in the guided‐waves analysis. In recent years, it has been pointed out that the Lorentz gauge condition and retarded potentials were formulated by Lorenz in 1867, much before the formulation of famous H. A. Lorentz [J.14, J.15]. However, most of the textbooks refer to the name of Lorentz. could be considered as the potential momentum per unit charge , just as the electric scalar potential ϕ is the potential energy per unit charge [J.16]. The potential momentum
could be considered as the potential momentum per unit charge , just as the electric scalar potential ϕ is the potential energy per unit charge [J.16]. The potential momentum 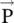 is obtained as follows:
is obtained as follows: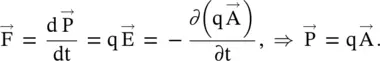
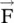 is the force acting on the charge q, and
is the force acting on the charge q, and 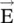 is given by equation ( 1.1.1b).
is given by equation ( 1.1.1b).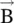 and
and 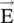 fields, the potentials
fields, the potentials 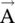 and ϕ could exist [B.11]. Aharonov–Bohm predicted that the potential fields
and ϕ could exist [B.11]. Aharonov–Bohm predicted that the potential fields 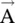 and ϕ, in the absence of
and ϕ, in the absence of 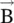 and
and 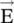 , could influence a charged particle. Tonomura and collaborators experimentally confirmed the validity of Aharonov–Bohm prediction. The Aharonov–Bohm effect demonstrates that
, could influence a charged particle. Tonomura and collaborators experimentally confirmed the validity of Aharonov–Bohm prediction. The Aharonov–Bohm effect demonstrates that 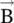 and
and 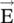 fields only partly describe the EM‐fields in quantum mechanics. The vector potential also has to be retained for a complete description of the EM‐field quantum mechanically [J.3, J.16, J.17]. However, to solve the classical electromagnetic problems, such as guided wave propagation and radiation from antenna, Heaviside formulation of Maxwell equations and potential functions as additional tools is adequate.
fields only partly describe the EM‐fields in quantum mechanics. The vector potential also has to be retained for a complete description of the EM‐field quantum mechanically [J.3, J.16, J.17]. However, to solve the classical electromagnetic problems, such as guided wave propagation and radiation from antenna, Heaviside formulation of Maxwell equations and potential functions as additional tools is adequate.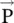 in dielectrics under the influence of the external electric field. Soon after the discovery of the electron in 1897 by J.J. Thomson, the models around electrons were developed to describe the electromagnetic properties of a material. Around 1898, John Gaston Leathem obtained an important relation
in dielectrics under the influence of the external electric field. Soon after the discovery of the electron in 1897 by J.J. Thomson, the models around electrons were developed to describe the electromagnetic properties of a material. Around 1898, John Gaston Leathem obtained an important relation 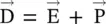 , connecting the displacement of charges in a material with polarization. Kelvin, in the year 1850, developed the concept of magnetic permeability and susceptibility with separate concepts of
, connecting the displacement of charges in a material with polarization. Kelvin, in the year 1850, developed the concept of magnetic permeability and susceptibility with separate concepts of 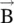 ,
, 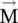 , and
, and  to characterize a magnetic material. In 1900, Drude developed the electrical conduction model, now known as the Drude model , after electron theory. Subsequently, the model was extended to the dielectric medium by Lorentz in 1905. The model called the Drude‐Lorentz model explains the dispersive property of dielectrics. In the year 1912, Debye developed the concept of dipole moment and obtained equations relating it to the dielectric constant. These models laid the foundation to study of the electric and magnetic properties of natural and engineered materials under the influence of external fields [B.4, B.6, B.7, B.12]
to characterize a magnetic material. In 1900, Drude developed the electrical conduction model, now known as the Drude model , after electron theory. Subsequently, the model was extended to the dielectric medium by Lorentz in 1905. The model called the Drude‐Lorentz model explains the dispersive property of dielectrics. In the year 1912, Debye developed the concept of dipole moment and obtained equations relating it to the dielectric constant. These models laid the foundation to study of the electric and magnetic properties of natural and engineered materials under the influence of external fields [B.4, B.6, B.7, B.12]










