1 Cover
2 Title page Geometric Modeling and Applications Set coordinated by Marc Daniel Volume 5
3 Copyright First published 2021 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2021 The rights of Christian Gentil, Gilles Gouaty and Dmitry Sokolov to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2021932086 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78630-040-9
4 Preface
5 Introduction
I.1. Fractals for industry: what for? I.2. Fractals for industry: how?
6 1 The BC-IFS Model 1.1. Self-similarity and IFS 1.2. Controlled Iterated Function System 1.3. Boundary controlled iterated function system
7 2 Design Examples 2.1. Curves 2.2. Wired structures 2.3. Surfaces and laces 2.4. Volumes and lacunar objects 2.5. Tree structures 2.6. Form assembly
8 3 Surface NURBS, Subdivision Surfaces and BC-IFS 3.1. Bezier curves and surfaces 3.2. Uniform B-spline curves and surfaces 3.3. Generalization 3.4. NURBS curves 3.5. Subdivision curves and surfaces
9 4 Building Operations, Assistance to Design and Applications 4.1. Topological consistency and symmetry constraints 4.2. Topological combination 4.3. Applications
10 Conclusion
11 Appendix: Data of FiguresA.1. Data of figures A.2. Subdivision surface in Figure 3.6
12 References
13 Index
14 Other titles from ISTE in Numerical Methods in Engineering
15 End User License Agreement
1 Introduction Figure I.1. 3D tree built by iterative modeling (source: project MODITERE no. AN...
2 Chapter 1 Figure 1.1. Schematic illustration of self-similarity. The black tree can be see... Figure 1.2. An example of a self-similar object composed of five copies of itsel... Figure 1.3. The self-similarity property, as shown in Figure 1.2, is symbolized ... Figure 1.4. Hausdorff distance. For a color version of this figure, see www.iste... Figure 1.5. Example of self-similarity involving non-contractive transformations... Figure 1.6. The Cantor set successively represented at the iteration levels from... Figure 1.7. Cartesian product of two Cantor sets successively represented at ite... Figure 1.8. The Sierpinski triangle successively represented at iteration levels... Figure 1.9. The Menger sponge successively represented at iteration levels from ... Figure 1.10. Example of Romanesco broccoli consisting of seven self-similar elem... Figure 1.11. On the left-hand side, we provide a few examples of self-similarity... Figure 1.12. Example of a decomposition of an L-shape into several similar eleme... Figure 1.13. Example of self-similarity. The object on the left-hand side has a ... Figure 1.14. Lattice structure of the attractors. On the left, the lattice struc... Figure 1.15. An example of a connection between two attractors. The green attrac... Figure 1.16. The evaluation tree of the attractor of the IFS computed at the thi... Figure 1.17. Example of the parameterization of the attractor in Figure 1.13. On... Figure 1.18. Example of a transport mapping that defines a morphism of IFS. For ...Figure 1.19. Example of mapping between two attractors using the transport map. ...Figure 1.20. Attractor defining the parameter space for the Sierpinski triangle ...Figure 1.21. Automaton of an IFS 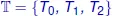 . The transition i is associated with the tran...Figure 1.22. Example of a three-state automaton inducing a restriction of the se...Figure 1.23. Both images represent the attractors defined from the same transfor...Figure 1.24. Other examples of attractors built from the same automatons as thos...Figure 1.25. Automaton generating the union of two attractors. Transitions 0 and...Figure 1.26. The internal structure of the Menger sponge. On the left, the inter...Figure 1.27. Automaton describing the structure of the image on the right-hand s...Figure 1.28. Example of a two-state automaton: the □ is divided into four △ and ...Figure 1.29. Construction of the sequence converging to the attractor of the aut...Figure 1.30. Approximation of the automaton attractor of Figure 1.28 obtained wi...Figure 1.31. Evaluation tree developed at level 2, for the attractor of the auto...Figure 1.32. Example of a third-degree B-spline surface defined from a grid of c...Figure 1.33. The surface, at the top right, is a smooth B-spline surface and has...Figure 1.34. Example of a curve constructed based on an FIF. The parallelepipeds...Figure 1.35. Barycentric space. On the left, the barycentric space of dimension ...Figure 1.36. Cantor set built in the barycentric space BI 2using the IFS compose...Figure 1.37. Sierpinski triangle built in the barycentric space BI 3. For a color...Figure 1.38. Example of projections of the Sierpinski triangle. The attractor is...Figure 1.39. Example of a two-state automaton. The □ is divided into three □ and...Figure 1.40. Three different projections of the attractor described by the autom...Figure 1.41. Automaton defining the attractor in the barycentric spaces and perf...Figure 1.42. Curve of the “Takagi” type, defined from three control points and t...Figure 1.43. Incidence constraints. On the left: Three curves of the “Takagi” ty...Figure 1.44. Example of the construction of a connection between the subdivision...Figure 1.45. Automaton integrating the cellular decomposition of a curve subdivi...Figure 1.46. Tree for a curve. For a color version of this figure, see www.iste....Figure 1.47. Quotient graph for a curve. For a color version of this figure, see...Figure 1.48. Example of curves generated for different parameter values. For a c...Figure 1.49. Attractor built from the IFS
. The transition i is associated with the tran...Figure 1.22. Example of a three-state automaton inducing a restriction of the se...Figure 1.23. Both images represent the attractors defined from the same transfor...Figure 1.24. Other examples of attractors built from the same automatons as thos...Figure 1.25. Automaton generating the union of two attractors. Transitions 0 and...Figure 1.26. The internal structure of the Menger sponge. On the left, the inter...Figure 1.27. Automaton describing the structure of the image on the right-hand s...Figure 1.28. Example of a two-state automaton: the □ is divided into four △ and ...Figure 1.29. Construction of the sequence converging to the attractor of the aut...Figure 1.30. Approximation of the automaton attractor of Figure 1.28 obtained wi...Figure 1.31. Evaluation tree developed at level 2, for the attractor of the auto...Figure 1.32. Example of a third-degree B-spline surface defined from a grid of c...Figure 1.33. The surface, at the top right, is a smooth B-spline surface and has...Figure 1.34. Example of a curve constructed based on an FIF. The parallelepipeds...Figure 1.35. Barycentric space. On the left, the barycentric space of dimension ...Figure 1.36. Cantor set built in the barycentric space BI 2using the IFS compose...Figure 1.37. Sierpinski triangle built in the barycentric space BI 3. For a color...Figure 1.38. Example of projections of the Sierpinski triangle. The attractor is...Figure 1.39. Example of a two-state automaton. The □ is divided into three □ and...Figure 1.40. Three different projections of the attractor described by the autom...Figure 1.41. Automaton defining the attractor in the barycentric spaces and perf...Figure 1.42. Curve of the “Takagi” type, defined from three control points and t...Figure 1.43. Incidence constraints. On the left: Three curves of the “Takagi” ty...Figure 1.44. Example of the construction of a connection between the subdivision...Figure 1.45. Automaton integrating the cellular decomposition of a curve subdivi...Figure 1.46. Tree for a curve. For a color version of this figure, see www.iste....Figure 1.47. Quotient graph for a curve. For a color version of this figure, see...Figure 1.48. Example of curves generated for different parameter values. For a c...Figure 1.49. Attractor built from the IFS 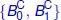 whose subdivision operators correspo...Figure 1.50. Subdivision structure of the tile. For a color version of this figu...Figure 1.51. Automaton for the subdivision of a quadrangular surface. For a colo...Figure 1.52. Cell structure of a quadrangular tile. For a color version of this ...Figure 1.53. Example of a quadrangular surface. For a color version of this figu...Figure 1.54. Example of a quadrangular surface bordered by Bezier curves with an...Figure 1.55. Example of a quadrangular surface structure bordered by Bezier curv...Figure 1.56. Example of a surface structure with fractal topology, obtained from...Figure 1.57. Example of the quadrangular surface bordered by Bezier curves with ...Figure 1.58. Example of curves projected into the modeling space
whose subdivision operators correspo...Figure 1.50. Subdivision structure of the tile. For a color version of this figu...Figure 1.51. Automaton for the subdivision of a quadrangular surface. For a colo...Figure 1.52. Cell structure of a quadrangular tile. For a color version of this ...Figure 1.53. Example of a quadrangular surface. For a color version of this figu...Figure 1.54. Example of a quadrangular surface bordered by Bezier curves with an...Figure 1.55. Example of a quadrangular surface structure bordered by Bezier curv...Figure 1.56. Example of a surface structure with fractal topology, obtained from...Figure 1.57. Example of the quadrangular surface bordered by Bezier curves with ...Figure 1.58. Example of curves projected into the modeling space 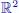 , following th...Figure 1.59. Example of curves projected into the modeling space
, following th...Figure 1.59. Example of curves projected into the modeling space 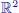 , following th...Figure 1.60. Example of curves projected into the modeling space
, following th...Figure 1.60. Example of curves projected into the modeling space 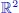 , following th...Figure 1.61. Example of a network of control points for a triangular surface tha...
, following th...Figure 1.61. Example of a network of control points for a triangular surface tha...
Читать дальше

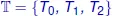 . The transition i is associated with the tran...Figure 1.22. Example of a three-state automaton inducing a restriction of the se...Figure 1.23. Both images represent the attractors defined from the same transfor...Figure 1.24. Other examples of attractors built from the same automatons as thos...Figure 1.25. Automaton generating the union of two attractors. Transitions 0 and...Figure 1.26. The internal structure of the Menger sponge. On the left, the inter...Figure 1.27. Automaton describing the structure of the image on the right-hand s...Figure 1.28. Example of a two-state automaton: the □ is divided into four △ and ...Figure 1.29. Construction of the sequence converging to the attractor of the aut...Figure 1.30. Approximation of the automaton attractor of Figure 1.28 obtained wi...Figure 1.31. Evaluation tree developed at level 2, for the attractor of the auto...Figure 1.32. Example of a third-degree B-spline surface defined from a grid of c...Figure 1.33. The surface, at the top right, is a smooth B-spline surface and has...Figure 1.34. Example of a curve constructed based on an FIF. The parallelepipeds...Figure 1.35. Barycentric space. On the left, the barycentric space of dimension ...Figure 1.36. Cantor set built in the barycentric space BI 2using the IFS compose...Figure 1.37. Sierpinski triangle built in the barycentric space BI 3. For a color...Figure 1.38. Example of projections of the Sierpinski triangle. The attractor is...Figure 1.39. Example of a two-state automaton. The □ is divided into three □ and...Figure 1.40. Three different projections of the attractor described by the autom...Figure 1.41. Automaton defining the attractor in the barycentric spaces and perf...Figure 1.42. Curve of the “Takagi” type, defined from three control points and t...Figure 1.43. Incidence constraints. On the left: Three curves of the “Takagi” ty...Figure 1.44. Example of the construction of a connection between the subdivision...Figure 1.45. Automaton integrating the cellular decomposition of a curve subdivi...Figure 1.46. Tree for a curve. For a color version of this figure, see www.iste....Figure 1.47. Quotient graph for a curve. For a color version of this figure, see...Figure 1.48. Example of curves generated for different parameter values. For a c...Figure 1.49. Attractor built from the IFS
. The transition i is associated with the tran...Figure 1.22. Example of a three-state automaton inducing a restriction of the se...Figure 1.23. Both images represent the attractors defined from the same transfor...Figure 1.24. Other examples of attractors built from the same automatons as thos...Figure 1.25. Automaton generating the union of two attractors. Transitions 0 and...Figure 1.26. The internal structure of the Menger sponge. On the left, the inter...Figure 1.27. Automaton describing the structure of the image on the right-hand s...Figure 1.28. Example of a two-state automaton: the □ is divided into four △ and ...Figure 1.29. Construction of the sequence converging to the attractor of the aut...Figure 1.30. Approximation of the automaton attractor of Figure 1.28 obtained wi...Figure 1.31. Evaluation tree developed at level 2, for the attractor of the auto...Figure 1.32. Example of a third-degree B-spline surface defined from a grid of c...Figure 1.33. The surface, at the top right, is a smooth B-spline surface and has...Figure 1.34. Example of a curve constructed based on an FIF. The parallelepipeds...Figure 1.35. Barycentric space. On the left, the barycentric space of dimension ...Figure 1.36. Cantor set built in the barycentric space BI 2using the IFS compose...Figure 1.37. Sierpinski triangle built in the barycentric space BI 3. For a color...Figure 1.38. Example of projections of the Sierpinski triangle. The attractor is...Figure 1.39. Example of a two-state automaton. The □ is divided into three □ and...Figure 1.40. Three different projections of the attractor described by the autom...Figure 1.41. Automaton defining the attractor in the barycentric spaces and perf...Figure 1.42. Curve of the “Takagi” type, defined from three control points and t...Figure 1.43. Incidence constraints. On the left: Three curves of the “Takagi” ty...Figure 1.44. Example of the construction of a connection between the subdivision...Figure 1.45. Automaton integrating the cellular decomposition of a curve subdivi...Figure 1.46. Tree for a curve. For a color version of this figure, see www.iste....Figure 1.47. Quotient graph for a curve. For a color version of this figure, see...Figure 1.48. Example of curves generated for different parameter values. For a c...Figure 1.49. Attractor built from the IFS 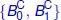 whose subdivision operators correspo...Figure 1.50. Subdivision structure of the tile. For a color version of this figu...Figure 1.51. Automaton for the subdivision of a quadrangular surface. For a colo...Figure 1.52. Cell structure of a quadrangular tile. For a color version of this ...Figure 1.53. Example of a quadrangular surface. For a color version of this figu...Figure 1.54. Example of a quadrangular surface bordered by Bezier curves with an...Figure 1.55. Example of a quadrangular surface structure bordered by Bezier curv...Figure 1.56. Example of a surface structure with fractal topology, obtained from...Figure 1.57. Example of the quadrangular surface bordered by Bezier curves with ...Figure 1.58. Example of curves projected into the modeling space
whose subdivision operators correspo...Figure 1.50. Subdivision structure of the tile. For a color version of this figu...Figure 1.51. Automaton for the subdivision of a quadrangular surface. For a colo...Figure 1.52. Cell structure of a quadrangular tile. For a color version of this ...Figure 1.53. Example of a quadrangular surface. For a color version of this figu...Figure 1.54. Example of a quadrangular surface bordered by Bezier curves with an...Figure 1.55. Example of a quadrangular surface structure bordered by Bezier curv...Figure 1.56. Example of a surface structure with fractal topology, obtained from...Figure 1.57. Example of the quadrangular surface bordered by Bezier curves with ...Figure 1.58. Example of curves projected into the modeling space 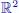 , following th...Figure 1.59. Example of curves projected into the modeling space
, following th...Figure 1.59. Example of curves projected into the modeling space 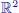 , following th...Figure 1.60. Example of curves projected into the modeling space
, following th...Figure 1.60. Example of curves projected into the modeling space 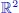 , following th...Figure 1.61. Example of a network of control points for a triangular surface tha...
, following th...Figure 1.61. Example of a network of control points for a triangular surface tha...










