There are a number of reasons why the story of scripting has not been told before. Among these:
1 – It's not mathematics, but software design, which is actually something that we do every day but not something that we usually write about.
2 – It's a complex and relatively long and winding story that cannot easily be summoned in a few punchlines. On top of this it contains subjects that most people haven't even heard about, such as visitors and pre‐processors.
3 – It's a hard sell to change conventional wisdom that scripting is only for exotics and has no relevance in post‐crisis finance. Actually, scripting is more relevant now than ever, because banks are under tough regulatory and cost pressures.
4 – It's very C++ and as such not following the current trend of lighter languages such as Matlab and Python backed by GPUs running parallel instructions in C.
5 – The subject is still very much alive: whenever we start documenting our efforts, we always get new ideas that we can do with scripting, which in turn tends to take away focus from documenting past glories.
My next employer is Saxo Bank and the scripting language there will be Jife.
Jesper Andreasen, June 2018
PART I A Scripting Library in C++
This part leads readers through the development steps of the scripting library provided in our source repository.
A transaction consists of a number of events occurring on given dates in the future. This is where a payment or coupon is fixed, a discrete barrier is monitored, or an exercise takes place. This is also where a path‐dependency is updated with reference to the simulated variables on that future date. 1 Future dates when such events take place are called event dates .
As an illustration, we consider a simplified version of the popular autocallable transaction. It pays a high coupon (say 10%) if some index (say S&P500) increased during the first year of its life. In this case, it pays the notional redemption together with the coupon of 10% and terminates at the end of year 1. Otherwise, it may still deliver a 20% coupon (10% per annum) at the end of year 2 provided the index overall increased over the two years. In this case, it repays the notional together with the 20% coupon and terminates at the end of year 2. If not, it is given a last chance on year 3, provided the underlying index increased over the three years. If this is the case, the investor receives the redemption + 30% at the end of year 3. If not, only 50% of the notional is repaid. It is easy to see that the investor implicitly sells a (somewhat exotic) option on what may appear as a low probability event (index decreasing over one, two, and three years) in exchange for a high coupon in a low‐yield environment, which explains the success of this structure. 2 This product may be scripted as follows (say today is 1 June 2020) 3 :
| 01Jun2020 |
vRef=spot() vAlive=1 |
| 01Jun2021 |
if spot() > vRef then prd=110 vAlive=0 endIf |
| 01Jun2022 |
if spot() > vRef then if vAlive=1 then prd=120 endIf vAlive=0 endIf |
| 01Jun2023 |
if vAlive=1 then if spot() > vRef then prd=130 else prd=50 endIf endIf |
We have four events on four event dates:
1 Today, we set the reference to the current spot level and initialize the alive status to 1.
2 Year 1, we check whether the spot increased, in which case we pay redemption + 10% and die.
3 Year 2, we check that the spot overall increased over two years. In this case, provided we survived year 1, we pay redemption + 20% and die.
4 Year 3, provided we survived the first two, we check if the spot overall increased. In this case we pay redemption + 30%. If not, we repay 50% of the notional.
We see that our language must at the very minimum support numbers, arithmetic operations, and conditional statements. We know we also need some mathematical functions like 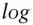 or
or 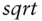 and some financial functions such as a multi‐argument
and some financial functions such as a multi‐argument 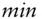 and
and 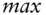 . Critically, we must be able to read, write, and compare variables and access the simulated market with a spot() keyword that references the fixing of the underlying asset on the corresponding event date. This is a simple language, similar to Python, that supports only the constructs necessary for the description of financial cash‐flows, for which it provides some specific keywords.
. Critically, we must be able to read, write, and compare variables and access the simulated market with a spot() keyword that references the fixing of the underlying asset on the corresponding event date. This is a simple language, similar to Python, that supports only the constructs necessary for the description of financial cash‐flows, for which it provides some specific keywords.
The language considers as a variable anything that starts with a letter and is not otherwise a keyword. We used the variables 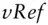 ,
, 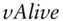 , and
, and 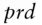 in our example. Evidently, ancillary variable names don't have to start with the letter V ; this is only for clarity.
in our example. Evidently, ancillary variable names don't have to start with the letter V ; this is only for clarity.
Products are variables . The language makes no difference between products and ancillary variables; only users do. Our example actually scripts three products: 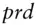 obviously;
obviously; 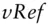 , which pays the spot fixing today and is worth today's underlying asset price; and
, which pays the spot fixing today and is worth today's underlying asset price; and 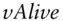 , which is worth 1 at maturity if the product survived the first two years, 0 otherwise. Its value is the (risk‐neutral) probability of surviving to year 3. All variables may be seen as products, although, in general, the values of ancillary variables are disregarded in the end. In chapter5, we will implement other means of distinguishing products from helper variables, and actual payments from assignments, with the keyword pays .
, which is worth 1 at maturity if the product survived the first two years, 0 otherwise. Its value is the (risk‐neutral) probability of surviving to year 3. All variables may be seen as products, although, in general, the values of ancillary variables are disregarded in the end. In chapter5, we will implement other means of distinguishing products from helper variables, and actual payments from assignments, with the keyword pays .
To value a script in the context of path‐wise Monte‐Carlo simulations means to evaluate it against a number of scenarios, each scenario providing different values for spot on the event dates in 1y, 2y, and 3y. For every such scenario generated by the model, we evaluate the script and record the final value of all its variables. In the end, we average those final variables' values across scenarios to estimate the values of the corresponding products. If we also require risk sensitivities, we compute the derivatives of the final variable values to changes in the model parameters. Evidently, the derivatives of prices are averages of the path‐wise derivatives, which permits an efficient path‐wise computations of sensitivities, in particular with adjoint propagation. See for instance Giles and Glasseman's “Smoking Adjoints,” which introduced adjoint techniques to finance [14], and our publication [27], which explains automatic adjoint differentiation (AAD) and provides professional differentiation code.
We remind the reader, however, that evaluation (including of sensitivities) is only one thing we can do with the script. The purpose of this library is to parse scripts into visitable data structures and implement a framework that enables all types of visitors, not only the evaluator, to traverse and manipulate scripts in many ways.
Читать дальше

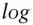 or
or 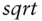 and some financial functions such as a multi‐argument
and some financial functions such as a multi‐argument 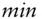 and
and 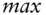 . Critically, we must be able to read, write, and compare variables and access the simulated market with a spot() keyword that references the fixing of the underlying asset on the corresponding event date. This is a simple language, similar to Python, that supports only the constructs necessary for the description of financial cash‐flows, for which it provides some specific keywords.
. Critically, we must be able to read, write, and compare variables and access the simulated market with a spot() keyword that references the fixing of the underlying asset on the corresponding event date. This is a simple language, similar to Python, that supports only the constructs necessary for the description of financial cash‐flows, for which it provides some specific keywords.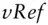 ,
, 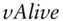 , and
, and 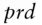 in our example. Evidently, ancillary variable names don't have to start with the letter V ; this is only for clarity.
in our example. Evidently, ancillary variable names don't have to start with the letter V ; this is only for clarity.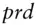 obviously;
obviously; 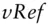 , which pays the spot fixing today and is worth today's underlying asset price; and
, which pays the spot fixing today and is worth today's underlying asset price; and 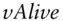 , which is worth 1 at maturity if the product survived the first two years, 0 otherwise. Its value is the (risk‐neutral) probability of surviving to year 3. All variables may be seen as products, although, in general, the values of ancillary variables are disregarded in the end. In chapter5, we will implement other means of distinguishing products from helper variables, and actual payments from assignments, with the keyword pays .
, which is worth 1 at maturity if the product survived the first two years, 0 otherwise. Its value is the (risk‐neutral) probability of surviving to year 3. All variables may be seen as products, although, in general, the values of ancillary variables are disregarded in the end. In chapter5, we will implement other means of distinguishing products from helper variables, and actual payments from assignments, with the keyword pays .










