El proceso sigue ocurriendo hasta que se encuentra el estado E 0y el símbolo de entrada «#» (última fila de la tabla) devuelve un símbolo vacío «-» y detiene el procesamiento de la máquina de Turing (estado H ). Por consiguiente, ya no hay ningún tipo de movimiento más por realizar. La computación se ha terminado.
Máquina de Turing universal
Una máquina de Turing universal U puede simular otra máquina de Turing T como una entrada. ¿Cómo lo logra? Leyendo (1) una descripción o tabla de instrucciones D t de la máquina E t a ser simulada y (2) los valores de entrada de dicha máquina E t . Pues bien, con esto se puede, con una sola máquina, lograr «ejecutar» cualquier otra máquina de Turing.
Esto lo representamos con la figura 1.3, donde una máquina de Turing universal U puede simular otra máquina de Turing E t con (1) descripción, (2) contenido y (3) estados. Esto conlleva la idea de que una máquina de Turing universal puede simular cualquier otra máquina de Turing dándole la información requerida en otra «cinta».

Figura 1.3 Una máquina de Turing universal.
Una máquina de Turing universal, concretamente, según dice Martin Davis, inspiró a John von Neumann para crear la primera arquitectura de computadoras en 1945, en su documento «First Draft of a Report on EDVAC» («Primer borrador de un informe sobre EDVAC»). En este documento, von Neumann presenta las ventajas del sistema binario sobre el decimal para las operaciones aritméticas elementales (+, -, ×, ÷), y según sus propias palabras, esto se explica por lo siguiente:
La principal virtud del sistema binario, en contraposición con el decimal, reside en la mayor simplicidad y velocidad con que se pueden ejecutar las operaciones elementales. (von Neumann, 1945)
Igualmente, se incorporan los registros especiales de memoria cuyo objetivo es, antes que nada, tener un conjunto de funciones ya definidas en memoria (por ejemplo: √, ||, log 10 , log 2 , ln , sin , etc.). Esto significa que no es necesario redefinir dichas funciones y, por ello, como es de suponer, el tiempo de cómputo se vería disminuido.
Por otro lado, el trabajo de Turing tuvo notables implicaciones en los fundamentos de la teoría de la complejidad computacional. Por su misma naturaleza, la capacidad explícita de secuencialidad de cada instrucción hace más simple poder clasificar problemas computacionales de acuerdo con su dificultad. Por ejemplo, las diversas clases de complejidad.
Antes de eso, primero debemos diferenciar dos cuestiones fundamentales: tiempo polinomial y tiempo exponencial. El tiempo polinomial, o mejor dicho, el tiempo polinomial de un algoritmo, es aquel en el que el tiempo de cómputo crece según la cantidad de datos de entrada n , los cuales no son exponenciales. Esto significa que la computación es más rápida. En la tabla 1.2se presentan varios algoritmos 4 clásicos, que usan la notación Big O 5 (en el peor de los casos):
| Tiempo polinomial |
Tiempo exponencial |
| Búsqueda lineal |
O ( n ) |
Knapsack 0/1 |
O (2 n ) |
| Búsqueda binaria |
O ( log n ) |
Travelling salesman problem |
O (2 n ) |
| Quicksort |
O ( n 2) |
Graph coloring |
O (2 n ) |
| Merge sort |
O ( n log n ) |
Hamylton cycle |
O (2 n ) |
Tabla 1.2 Comparación de complejidad algorítmica entre tiempo polinomial y tiempo exponencial.
Cualquier algoritmo que tenga una complejidad elevada a la enésima potencia (como los que aparecen en la columna de la derecha) es computacionalmente demasiado complejo de solucionar en un tiempo de cómputo óptimo (polinomial). Esto se traduce en que se tarda demasiado tiempo en terminar la computación.
Pasemos a ver las principales clases de complejidad:
• P ( polynomial en inglés). Es la clase de problema que es posible tratar, es decir, hay un algoritmo determinístico que lo resuelve de manera eficiente en un tiempo polinomial. Por ejemplo, los algoritmos de ordenamiento y de búsqueda de una subcadena dentro de un texto o del camino más corto entre dos nodos dentro de un grafo, entre otros.
• NP ( non-deterministically polynomial en inglés). La clase de problemas que pueden ser resueltos en un tiempo polinomial por un algoritmo no determinístico. (Esto último significa que son algoritmos que tienen un componente de selección aleatorio en su comportamiento, es decir, cada ejecución con los mismos argumentos no asegura el mismo valor de devolución. Por ejemplo, el algoritmo de colonia de hormigas, algoritmos genéticos, etc.) Los problemas NP son problemas de decisión. De esta clase nace la siguiente pregunta: ¿estos problemas pueden resolverse de manera determinista en un tiempo polinomial? Es decir, ¿es P = NP ? Esto no ha sido probado y es uno de los problemas del siglo que aún sigue abierto. Ejemplos de problemas de esta clase: la factorización de números enteros y el isomorfismo de grafos.
• NP-Completo. Problemas más difíciles que los NP y, obviamente, que los P. Son problemas de decisión que se diferencian de los NP en lo siguiente: representan el conjunto de todos los problemas X en NP que se pueden reducir a cualquier otro problema NP en tiempo polinomial, es decir, intuitivamente lo entendemos así: si tenemos la solución para el problema X , entonces podríamos encontrar rápidamente la solución al problema Z . Ejemplos de problemas de esta clase son: 3-SAT, el problema del vendedor viajero, camino hamiltoniano, etc.
• NP-Difícil ( NP-hard en inglés). Son problemas de decisión tan complejos como los NP, pero no se sabe si existe un algoritmo verificable en tiempo polinomial para todos los casos. Esto último nunca ha sido demostrado, es decir, si P ≠ NP , entonces los problemas de esta categoría no pueden ser resueltos en tiempo polinomial. Un ejemplo de este tipo es el problema de la parada, que es NP-Difícil pero no NP-Completo.
La figura 1.4resume la relación entre estas tres clases de complejidad:
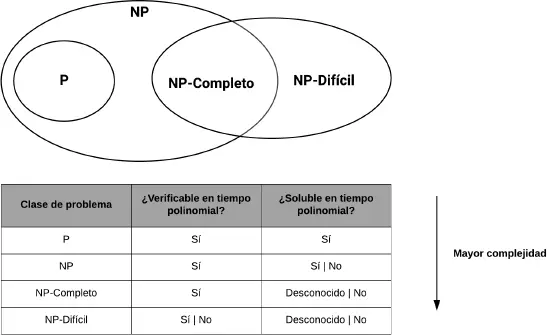
Figura 1.4 Características de cada clase de problema de complejidad. El signo «|» significa «o».
Resumiendo, las clases de complejidad existen porque hay muchos tipos de problemas computacionales y una forma de tratarlos de mejor manera es clasificarlos por su dificultad. Con esto es posible diseñar técnicas algorítmicas más adecuadas según su clase.
El cálculo lambda es un modelo de computación que está basado en funciones computables. Fue creado por Alonzo Church y lo veremos con mayor detalle en la parte IIdel libro ( capítulo 4), pero aquí daremos un esbozo general del modelo. Al igual que Alan Turing con su máquina de Turing, el cálculo lambda de Alonzo Church probó negativamente el problema de decisión.
A diferencia de la máquina de Turing, que tiene un proceso secuencial, el cálculo lambda construye la computación a través de funciones computables que se forjan en una notación formal con una gran expresividad. El cálculo lambda es una máquina de recursividad que cuenta con operadores, variables y operaciones de reducción (conocida como reducción b). Por tanto, hace un uso asiduo de la recursividad y de mantener estados inmutables en cada una de sus fases de reducción o derivación.
Читать дальше