Stephen Winters-Hilt - Informatics and Machine Learning

Figure 1.2 The Viterbi path. (Left) The Viterbi path is recursively defined, thus tabulatable, with one column only, recursively, dependent on the prior column. (Right) A related recursive algorithm used to perform sequence alignment extensions with gaps (the Smith–Waterman algorithm) is provided by the neighbor‐cell recursively‐defined relation shown.

HMMs, unlike tFSAs, have a straightforward mathematical and computational foundation at the nexus where Bayesian probability and Markov models meet dynamic programming. To properly define or choose the HMM model in a ML context, however, further generalization is usually required. This is because the “bare‐bones” HMM description has critical weaknesses in most applications, which are described in Chapter 7, along with their “fixes.”Fortunately, each of the standard HMM weaknesses can be addressed in computationally efficient ways. The generalized HMMs described in Chapter 7allow for a generalized Viterbi Algorithm (see Figure 1.2) and a generalized Baum–Welch Algorithm. The generalized algorithms retain path probabilities in terms of a sequence of likelihood ratios, which satisfy Martingale statistics under appropriate circumstances [102] , thereby having Martingale convergence properties (where here convergence is associated with “learning” in this context). Thus, HMM learning proceeds via convergence to a limit state that provably exists in a similar sense to that shown with the Hoeffding inequality [59] , via its proven extension to Martingales [108] . The Hoeffding inequality is a key part of the VC Theorem in ML, whereby convergence for the Perceptron learning process to a solution in an infinite solution space is proven to exist in a finite number of learning steps [109] . Further details on the Fundamental Theorems [102, 103, 108, 109] are summarized in Appendix C.

HMM tools have recently been developed with a number of computationally efficient improvements (described in detail in Chapter 7), where application of the HMM methods will be described for gene‐finding, alt‐splice gene‐finding, and nanopore‐detector signal analysis.

HMM methods are powerful, especially with the enhancements described in Chapter 7, but this would all be for naught in a real‐time, O(L), processing on L size data if the core O(L N 2) algorithm ( N states in the HMM) could not be distributed, onto O( N 2) nodes, say, to get back to an overall distributed process involving HMM feature extraction with O(L) processing (to be part of our real‐time signal processing pipeline). So, a way is needed to distribute the core algorithms for HMM learning: Viterbi and Baum–Welch. It turns out distributed processing, or “chunking,” is possible for the single sweep Viterbi algorithm (ignoring the trivial traceback optimal path recovery that does not cause table alteration). The key to having this chunking capability on the other core learning algorithm, Baum–Welch, is to have a similar single‐pass table production. The standard Baum–Welch requires a forward and a backward sweep across the table during production of the result (with algorithms named accordingly for this purpose in Chapter 3). As this would disallow the chunking solution, what is needed is a single sweep Baum Welch algorithm, which has been discovered and is described in Chapter 3, where it is known as the Linear Memory HMM (at the time of its discovery it was most notable to reviewers due to another oddity, that it required only linear space memory during computation – but memory is cheap, while being able to perform distributed processing with massive speed‐up operationally is much more important). With distributability (asynchronous), computational time is directly reduced by ~ N on a cluster with N nodes (see Figure 1.2). The HMM with single‐sweep Linear Memory (distributable) for expectation/maximization (EM) also allows distribution (massive parallel asynchronous processing) for the generalized Viterbi and Baum–Welch algorithms on the Meta‐HMM and Hidden Markov model‐with‐duration (HMMD) variants described in Chapter 3with distribution shown in ( Figure 1.3).

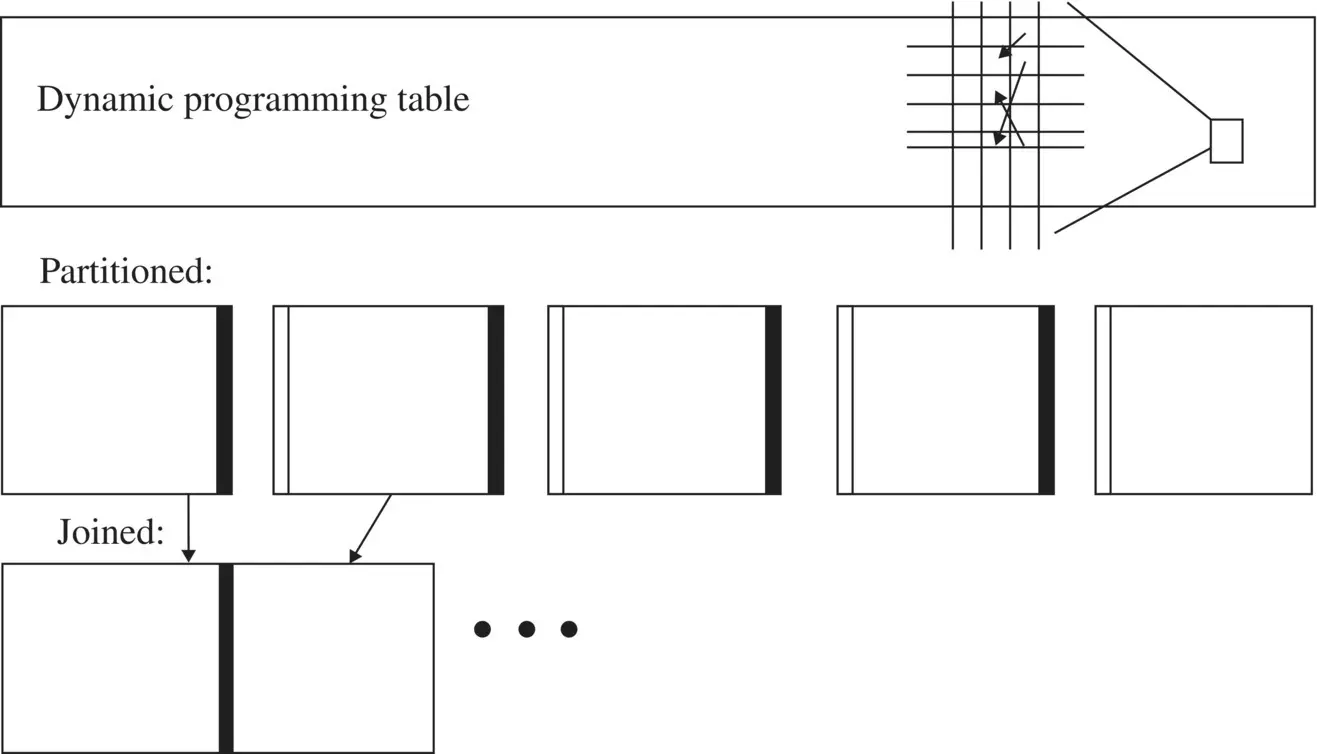
Figure 1.3 Chunking on a dynamic table. Works for a HMM using a simple join recovery.

The main application areas for HMMs covered in this book are power signal analysis generally, and bioinformatics and cheminformatics specifically (the main reviews and applications discussed are from [128–134]). For bioinformatics, we have information encoding molecules that are polymers, giving rise to sequential data format, thus HMMs are well suited for analysis. To begin to understand bioinformatics, however, we need to know not only the biological encoding rules, largely rediscovered on the basis of their statistical anomalies in Chapters 1– 4, but also the idiosyncratic structures seen (genomes and transcriptomes) that are full of evolutionary artifacts and similarities to evolutionary cousins. To know the nature of the statistical imprinting on the polymeric encodings also requires an understanding of the biochemical constraints that give rise to the statistical biases seen. Once taken altogether, bioinformatics offers a lot of clarity on why Nature has settled on the particular genomic “mess,” albeit with optimizations, that it has selectively arrived at. See [1, 3] for further discussion of bioinformatics.

The prospect of having a HMM feature extraction in the streaming signal processing pipeline (O(L), for size L data process) offers powerful real‐time feature extraction capabilities and specialized filtering (all of which is implemented in the Nanoscope, Chapter 14). One such processing method, described in Chapter 6, is HMM/Expectation Maximization (EM) EVA (Emission Variance Amplification) Projection which has application in providing simplified automated tFSA Kinetic Feature Extraction from channel current signal. What is needed is the equivalent of low‐pass filtering on blockade levels while retaining sharpness on the timing of the level changes. This is not possible with the standard low‐pass filter because the edges get blurred out in the local filtering process, but notice how this does not happen with the HMM‐based filter, for the data shown in Figure 1.4.

HMM is a common intrinsic statistical sequence modeling method (implementations and applications are mainly drawn from [135–158] in what follows), so the question naturally arises – how to optimally incorporate extrinsic “side‐information” into a HMM? This can be done by treating duration distribution information itself as side‐information and a process is shown for incorporating side‐information into a HMM. It is thereby demonstrated how to bootstrap from a HMM to a HMMD (more generally, a hidden semi‐Markov model or HSMM, as it will be described in Chapter 7).

In many applications, the ability to incorporate the state duration into the HMM is very important because conventional HMM‐based, Viterbi and Baum‐Welch algorithms are otherwise critically constrained in their modeling ability to distributions on state intervals that are geometric (this is shown in Chapter 7). This can lead to a significant decoding failure in noisy environments when the state‐interval distributions are not geometric (or approximately geometric). The starkest contrast occurs for multimodal distributions and heavy‐tailed distributions, the latter occurring for exon and intron length distributions (thus critical in gene finders). The hidden Markov model with binned duration (HMMBD) algorithm eliminates the HMM geometric distribution modeling constraint, as well as the HMMD maximum duration constraint, and offers a significant reduction in computational time for all HMMBD‐based methods to be approximately equal to the computational time of the HMM‐process alone .