S. R. Kingan - Graphs and Networks

1 Cover

2 Title Page Graphs and Networks S. R. Kingan Brooklyn College and The Graduate Center, City University of New York, New York, NY, USA.

3 Copyright

4 Dedication

5 List of Figures

6 Preface

7 1 From Königsberg to Connectomes 1.1 Introduction 1.2 Isomorphism 1.3 Constructions and Minors Exercises Topics for Deeper Study Notes

8 2 Fundamental Topics 2.1 Trees 2.2 Distance 2.3 Degree Sequences 2.4 Matrices Exercises Topics for Deeper Study Notes

9 3 Similarity and Centrality 3.1 Similarity Measures 3.2 Centrality Measures 3.3 Eigenvector and Katz Centrality 3.4 PageRank Exercises Topics for Deeper Study Notes

10 4 Types of Networks 4.1 Small‐World Networks 4.2 Scale‐Free Networks 4.3 Assortative Mixing 4.4 Covert Networks Exercises Topics for Deeper Study Notes

11 5 Graph Algorithms 5.1 Traversal Algorithms 5.2 Greedy Algorithms 5.3 Shortest Path Algorithms Exercises Topics for Deeper Study Notes

12 6 Structure, Coloring, Higher Connectivity 6.1 Eulerian Circuits 6.2 Hamiltonian Cycles 6.3 Coloring 6.4 Higher Connectivity 6.5 Menger's Theorem Exercises Topics for Deeper Study Notes

13 7 Planar Graphs 7.1 Properties of Planar Graphs 7.2 Euclid's Theorem on Regular Polyhedra 7.3 The Five Color Theorem 7.4 Invariants for Non‐planar Graphs Exercises Topics for Deeper Study Notes

14 8 Flows and Matchings 8.1 Flows in Networks 8.2 Stable Sets, Matchings, Coverings 8.3 Min–Max Theorems 8.4 Maximum Matching Algorithm Exercises Topics for Deeper Study Notes

15 Appendix A: Linear Algebra

16 Appendix B: Probability and Statistics

17 Appendix C: Complexity of Algorithms Notes

18 Appendix D: Stacks and Queues

19 Bibliography

20 Index

21 End User License Agreement

1 Chapter 1 Figure 1.1 The bridges of Königsberg. Figure 1.2 The prism graph. Figure 1.3 An example of a graph, multigraph, digraph, and network. Figure 1.4 Traveling salesman network. Figure 1.5 Strongly connected digraphs. Figure 1.6 Complete graphs. Figure 1.7 Paths, cycles, and wheels. Figure 1.8 Bipartite and tripartite graphs. Figure 1.9 Star graphs. Figure 1.10 Example of trees. Figure 1.11 Subgraphs. Figure 1.12 Two drawings of a planar graph. Figure 1.13 C. elegans connectome. Figure 1.14 C. elegans in‐degree (top) and out‐degree (bottom) distributions... Figure 1.15 Three pairs of isomorphic graphs. Figure 1.16 The non‐isomorphic graphs on 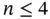vertices. Figure 1.17 The non‐identical graphs on 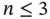vertices. Figure 1.18 Shapes of graphs. Figure 1.19 The Erdős‐1 collaboration graph. Figure 1.20 Two non‐isomorphic graphs and their decks of vertex‐deletions. Figure 1.21 An example of a join. Figure 1.22 Two examples of Cartesian products. Figure 1.23 The four‐dimensional cube. Figure 1.24 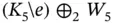and . 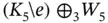Figure 1.25 Examples of complements. Figure 1.26 Examples of a subdivision. Figure 1.27 Line graphs. Figure 1.28 Forbidden induced subgraphs for line graphs. Figure 1.29 Example of edge‐deletions and edge‐contractions. Figure 1.30 Petersen graph. Figure 1.31 Examples of graphs and digraphs. Figure 1.32 Pairs of graphs for isomorphism testing. Figure 1.33 A graph that contains all nine forbidden induced subgraphs for l...

2 Chapter 2Figure 2.1 Non‐isomorphic trees on 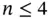vertices.Figure 2.2 Spanning trees.Figure 2.3 An example for Cayley's tree counting theorem.Figure 2.4 A tree with a left and right vertex.Figure 2.5 Eccentricity, diameter, and radius.Figure 2.6 Cut vertices and bridges.Figure 2.7 Cospectral graphs with respect to the adjacency matrix.Figure 2.8 Examples of graphs and digraphs.Figure 2.9 Three pairs of cospectral graphs.

3 Chapter 3Figure 3.1 Customer‐item bipartite graph.Figure 3.2 A graph and a digraph for centrality measures.Figure 3.3 A graph and a digraph.Figure 3.4 Schoch and Brandes graphs.Figure 3.5 A small town map.

4 Chapter 4Figure 4.1 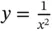with a standard scale and a log–log scale.Figure 4.2 The in‐degree distribution of the high energy physics citation di...Figure 4.3 Classification of 1958 couples based on race.Figure 4.4 Assortativity function for the Erdős‐1 collaboration graph.Figure 4.5 Regional Schools Network and Organizations Network.

5 Chapter 5Figure 5.1 Step‐by‐step explanation of DFS and BFS.Figure 5.2 Kruskal's and Prim's algorithms.Figure 5.3 A Weighted Digraph.Figure 5.4 Dijkstra's Algorithm.Figure 5.5 Examples of weighted graphs.Figure 5.6 Example of a weighted digraph.

6 Chapter 6Figure 6.1 Hierholzer's algorithm.Figure 6.2 Eulerizing graphs.Figure 6.3 Hamiltonian graphs.Figure 6.4 Kirkman's graph and 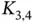.Figure 6.5 Non‐Hamiltonian graphs.Figure 6.6 Closure of a graph.Figure 6.7 Graph coloring.Figure 6.8 Greedy Coloring Algorithm.Figure 6.9 Vertex and edge connectivity.Figure 6.10 Ear decompositions.Figure 6.11 An example for Menger's TheoremFigure 6.12 Deletion and contraction of the edges of .

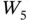7 Chapter 7Figure 7.1 Stereographic projection.Figure 7.2 Geometric dual.Figure 7.3 Non‐isomorphic graphs with isomorphic geometric duals.Figure 7.4 Schlegel diagram of a cube.Figure 7.5 Graphs that do not correspond to convex polyhedra.Figure 7.6 Platonic solids.Figure 7.7 Tutte's counterexample to Tait's conjecture.Figure 7.8 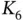with 3 edge crossings.Figure 7.9 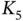embedded on the torus.

8 Chapter 8Figure 8.1 Network flows.Figure 8.2 Flow augmenting path.Figure 8.3 Stable sets, matchings, and coverings.Figure 8.4 A system of distinct representatives.Figure 8.5 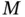‐augmenting path.Figure 8.6 Matchings and blossoms.Figure 8.7 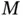‐alternating trees.Figure 8.8 Flower.Figure 8.9 A graph with a matching.Figure 8.10 A graph with a larger matching.

9 4Figure D.1 Example of a stack.Figure D.2 Example of a queue.

1 Cover Page

2 Table of Contents

3 Title Page Graphs and Networks S. R. Kingan Brooklyn College and The Graduate Center, City University of New York, New York, NY, USA.

4 Copyright

5 Dedication

6 List of Figures

7 Preface

8 Begin Reading

9 Appendix A Linear Algebra

10 Appendix B Probability and Statistics

11 Appendix C Complexity of Algorithms