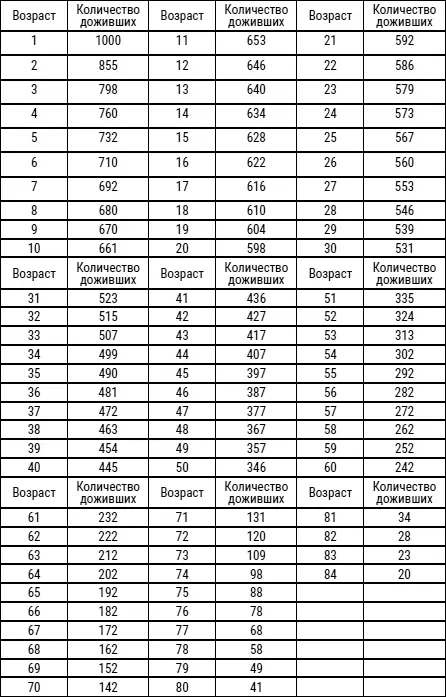
Таблица жизни Галлея
Какой же смертный, я вас спрашиваю, в состоянии оценить количество недугов, происходящих ото всех возможных причин, которые поражают тело человека в каждую из множества его частей и в любом возрасте, и сказать, с какой вероятностью смертельным окажется то или иное заболевание… и на этом основании делать предсказания о соотношении жизни и смерти в грядущих поколениях?
Заключив, что это и подобные предсказания «зависят от условий, которые полностью скрыты от нас, и постоянно обманывают наши чувства бесконечной сложностью своих взаимодействий», Бернулли также предлагает статистический (вероятностный) подход.
Впрочем, есть и другой способ, который приведет нас к искомому и даст возможность по крайней мере a posteriori оценить то, что мы не можем определить a priori , то есть оценить это по результатам, наблюдаемым во множестве других случаев. В этой связи следует предположить, что при сходных условиях то, что событие состоится (или не состоится) в будущем, будет следовать той же закономерности, которая наблюдалась для похожих событий в прошлом. Например, если мы наблюдали, что из 300 человек одного возраста и той же конституции, как некто Тициус, 200 умерли в течение десяти лет, а остальные остались жить, мы можем с разумной уверенностью заключить, что шансов, что Тициус вынужден будет уплатить долг природе в течение ближайшей декады, вдвое больше, чем шансов, что он проживет дольше этого времени.
Свои математические выкладки, касающиеся смертности, Галлей завершил интересным замечанием более философского толка. Особенно трогателен один абзац.
Помимо применений, описанных выше, вероятно, было бы, пожалуй, позволительно выводить из тех же самых Таблиц, сколь несправедливо мы ропщем на быстротечность жизни и думаем, будто нас обделили, если мы не достигли старости, поскольку из Таблиц явствует, что половина тех, кто появляется на свет, умирает до достижения семнадцати лет: 1238 к тому времени сокращается до 616. Так что вместо того, чтобы сетовать на так называемую безвременную смерть, мы должны со смирением и равнодушием покориться распаду – неизбежному свойству бренного вещества, из которого мы состоим, и нашей хрупкой и прекрасной структуры и состава, и быть искренне благодарными за то, что пережили – причем зачастую на много лет – тот период, до которого не доживает половина всего рода человеческого.
Хотя положение в большей части современного мира по сравнению с печальной статистикой Галлея заметно улучшилось, к сожалению, так обстоят дела не во всех странах. Например, в Замбии уровень смертности детей до пяти лет в 2006 году достиг чудовищной цифры в 182 смерти на 1000 живых новорожденных. И ожидаемая продолжительность жизни в Замбии так низка, что сердце сжимается: всего тридцать семь лет.
Однако статистика занимается не только смертями. Она проникает во все аспекты человеческой жизни – от чисто физических черт до плодов интеллектуального труда. То, что статистика, потенциально способна порождать «законы» для общественных наук, первым понял бельгийский ученый-энциклопедист Ламбер-Адольф-Жак Кетле (1796–1874). Именно ему мы и обязаны введением общестатистического понятия «среднего человека».
Адольф Кетле родился 22 февраля 1796 года в древнем бельгийском городе Генте [86] Две прекрасные книги о Кетле и его трудах – Hankins 1908 и Lottin 1912. Относительно лаконичные, но, тем не менее, информативные заметки можно найти в Stigler 1997, Krüger 1987 и Cohen 2006.
. Его отец, городской чиновник, умер, когда Адольфу было всего семь лет. Кетле был вынужден сам зарабатывать себе на жизнь и уже в 17 лет стал преподавать математику. В свободные от учительских обязанностей время он сочинял стихи, написал либретто оперы, поучаствовал в создании двух пьес и перевел несколько художественных произведений. При всем при том его любимым предметом осталась математика, и он первым закончил Гентский университет со степенью доктора наук. В 1820 году Кетле был избран членом Королевской академии наук в Брюсселе и вскоре стал принимать активнейшее участие в ее деятельности. Следующие несколько лет были посвящены в основном преподаванию и публикации нескольких трактатов по математике, физике и астрономии.
Первую лекцию по истории науки Кетле обычно начинал следующим глубоким наблюдением: «Чем сильнее развиваются науки, тем дальше они вступают в сферу влияния математики, которая становится словно бы центром, к которому они стягиваются. О том, какого совершенства достигла та или иная наука, можно судить по тому, с какой легкостью ее результаты можно получить путем вычисления».
Читать дальше
Конец ознакомительного отрывка
Купить книгу













