Марио Ливио - Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса

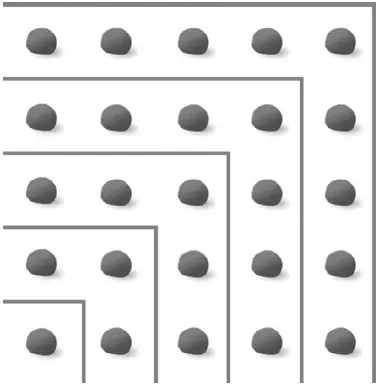
Рис. 2

Квадраты целых чисел, которые ассоциируются с гномонами, вероятно, привели Пифагора и к формулировке его знаменитой теоремы. Это прославленное математическое утверждение гласит, что у любого прямоугольного треугольника площадь квадрата, достроенного на самой длинной стороне – гипотенузе, равна сумме площадей квадратов, достроенных на двух других сторонах – катетах (рис. 3). Карикатуристы под псевдонимом «Франк и Эрнест» посвятили истории открытия теоремы смешную картинку (рис. 4). Как видно на рис. 2, если добавить к квадрату 4 × 4 гномон 9 = 3 2, получится новый квадрат 5 × 5, то есть 3 2+ 4 2= 5 2. Поэтому числа 3, 4, 5 могут быть длинами сторон прямоугольного треугольника. Наборы целых чисел, обладающие этим свойством (например, 5, 12, 13, поскольку 5 2+ 12 2= 13 2), называются пифагоровыми тройками.

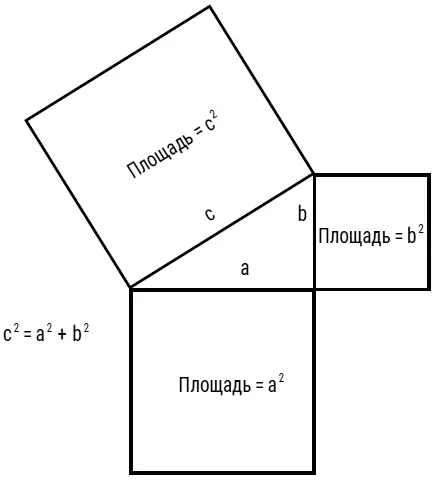
Рис. 3

Рис. 4

Мало какие математические теоремы могут похвастаться такой «узнаваемостью», как теорема Пифагора. В 1971 году, когда республика Никарагуа выбирала «десять математических формул, изменивших облик планеты» для коллекционной серии марок, теорема Пифагора появилась на второй марке (рис. 5); на первой значилось «1 + 1 = 2»).

Однако был ли Пифагор первым, кто сформулировал широкоизвестную теорему, которую ему приписывают? Некоторые древнегреческие историки в этом не сомневались. В комментарии к «Началам» Евклида (ок. 325–265 гг. до н. э.) – пространному труду по геометрии и теории чисел – греческий философ Прокл (ок. 411–485) писал: «Если мы захотим послушать тех, кто любит записывать древности, мы узнаем, что они приписывают эту теорему Пифагору и сообщают, что он принес в жертву быка за свое открытие» ( здесь и далее пер. А. Щетникова ) [11] Обратите внимание, что в этом комментарии Прокл ничего не говорит о собственных представлениях о том, был ли Пифагор первым, кто сформулировал эту теорему. История о быке упоминается в трудах Диогена Лаэрция, Порфирия и историка Плутарха (ок. 46–120 гг.). Все эти рассказы восходят к Аполлодору. Однако там говорится лишь о каком-то «знаменитом утверждении» и не уточняется, о каком именно утверждении идет речь. См. Laertius ca. 250 AD, Plutarch ca. 75 AD. . Однако пифагоровы тройки изображены и на вавилонской клинописной табличке Plimton 322, которая датируется куда более ранним временем – приблизительно династией Хаммурапи (ок. 1900–1600 гг. до н. э.). Более того, геометрические конструкции, основанные на теореме Пифагора, обнаружены и в Индии, где этим соотношением пользовались при строительстве алтарей. Несомненно, о них знал и автор «Шатапатха-брахманы», комментария к древнеиндийским священным текстам, созданного, вероятно, по меньшей мере за несколько веков до Пифагора (Renon and Felliozat 1947, van der Waerden 1983). Впрочем, не так уж важно, первым ли Пифагор сформулировал теорему, получившую его имя, – главное, что постоянно обнаруживавшая себя разного рода взаимосвязь между числами, формами и Вселенной еще на шаг приблизила пифагорейцев к детальной метафизике порядка.

Рис. 5

Важнейшую роль в пифагорейском мире играла и другая идея – понятие о космических противоположностях. Поскольку система противоположностей была основным принципом ранней ионийской научной школы, было естественно, что ее приняли пифагорейцы с их одержимостью порядком. Более того, Аристотель рассказывает, что с идеей, что все на свете уравновешено, поскольку организовано в пары, соглашался даже врач по имени Алкмеон, живший в Кротоне в те годы, когда там существовала знаменитая школа Пифагора. Главная пара противоположностей состояла из предела , выраженного нечетными числами, и беспредельного , выраженного четными. Предел есть сила, наводящая порядок и гармонию в диком необузданном беспредельном. И хитросплетения Вселенной в целом, и перипетии человеческой жизни на уровне микрокосма, как полагали пифагорейцы, состоят из пар противоположностей, которые так или иначе соотносятся друг с другом, и управляются этими противоположностями. Эта несколько черно-белая картина мира описывалась «таблицей противоположностей», которая приведена в «Метафизике» Аристотеля: