Абрахам Меррит - Мир приключений, 1929 № 05-06

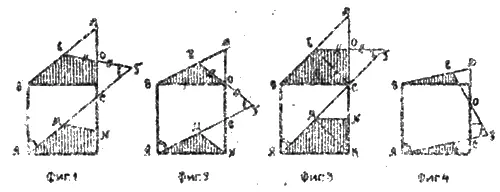
На фиг. 2 и 3 изображены решения при крайних положениях секущей: на фиг. 2 точка С находится в середине стороны квадрата, а на фиг. 3 — в противоположном углу квадрата (все буквенные обозначения остаются прежние). Для таких предельных случаев легко определить величину углов трапеции (в последнем случае углы при большом основании очевидно равны 45°; здесь возможно и другое деление квадрата по долям, если вместо MN провести МК). Верное геометрическое решение получается и в том случае, если секущая АС пересечет противоположную сторону ниже ее середины (фиг. 4.) но такое решение не удовлетворяет требованиям задачи, так как при нем получается в квадрате и в трапеции по 4 доли вместо трех. Предлагаем самим читателям продолжить и закончить исследование такого решения при различных положениях точки С на продолжении правой стороны квадрата (см. фиг. 5)

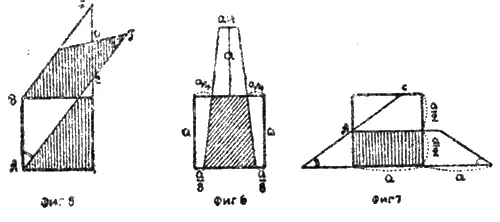
Для второй половины задачи есть тоже очень много решений — при том же числе дробимых долей. Одним из наиболее простых будет тот случай, когда высота трапеция берется равной удвоенной стороне или половине стороны квадрата (см. фиг. 6 и 7)

Вагон оборудован нецелесообразно, так как все бидоны, прислоненные к стенкам за ними (считая по направлению движения поезда) будут при резких торможениях или остановках скидываться вниз. Целесообразнее делать стелажи не поперек вагона, а вдоль его. — Для робких пассажиров, ездящих в поездах курьерских и тихоходах, есть некоторый смысл выбирать вагоны в первом случае в хвосте поезда (их меньше шансов нагнать сзади), а во втором случае — в голове поезда. Применительно к молоку, независимо от шансов на крушение, для обезопасения от толчков при резких торможениях или остановках лучше садиться спиной к направлению движения (лежать на нижних полках сравнительно безопаснее, чем на верхних).

Старик выяснил сперва, что в подземелье ость строго прямолинейный путь. Для этого он сделал проверку: спустившись в колодце, он оставил у стены зажженный фонарь, а затем поднялся, обошел по горе к выходу, и, войдя в подземелье, убедился, что свет фонаря ясно виден с того примерно места, где на схеме пунктирный проход делает поворот под прямым углом. Пройдясь потом по подземелью до колодца, строго держась все время на свет фонаря, он нащупал в самом конце, справа от себя, выступ степы ближайшей к колодцу пещеры и тщательно измерил расстояние от этого выступа до фонаря. При дальнейших спусках в подземелье, старик всегда ставил свой фонарь строго на прежнее-же место у стены и, пятясь от него назад, без особых трудов доходил до первого выступа стены (тоже справа от себя): а после того он преходил тем-же рачьим способом и весь путь, проверяя все время створу темного выступа степы на освещенный фонарь. Для удобства обратного следования по подземелью, он стал ставить еще в самом угле поворота маршрута зеркальце, чтобы свет фонаря отражался-бы при самом входе в подземелье из долины.

Если обозначить через а гипотенузу данного треугольника, через А— тот катет, в сторону которого делается построение, через с — второй катет и через h1, h2, h3 и т. д. — последовательно все проводимые перпендикуляры, то можно написать такие пропорции: h1: с = b: с; h2: h1 = b: а; h2: h3 = b: a; h1: h3 = b: a и т. д. Отсюда ясно, что ряд h1, h2, h3, h4, .…. представляет собой бесконечно убывающую геометрическую прогрессию, знаменатель которой есть Ь: а (меньше 1). Сумма такой прогрессии как доказывается в алгебре, равняется частному от делению первого члена прогрессии на разность между единицей и знаменателем прогрессии. Значит: h1+h2+h3+h4 +….. = (bс: а):(1-b: а) = bс: (а-b). По условию последняя величина равняется периметру a+b+с. Из ур-ний:

1) a+b+c = bс: (a-b) и 2) а 2 = b 2+с 2 находим соотношения между сторонами: это можно сделать, напр., после приравнения одной стороны, напр. а, к единице. Из решения уравнений получим, что в таком случае b = 4: 5, а с = 3:5, пли что а: b: с — 5:4:3. Следовательно, условию задачи удовлетворяет любой египетский треугольник.

Правильное решение этой задачи прислала подписчики Э. Эллер, Б. Скрябин и М. Г. Грикуров.