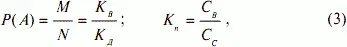Ольга Скачкова - Страхование - конспект лекций

Методики расчёта тарифных ставок утверждены Федеральной службой страхового надзора (прежнее наименование – Росстрахнадзор). Общий принцип расчета нетто-ставки состоит в следующем. Методика расчёта нетто-ставки по каждому виду страхования, сводится к определению среднего показателя убыточности страховой суммы, за тарифный период (5 или 10 лет с поправкой на величину действия надбавки). В основе определения нетто-ставки по любому виду страхования лежит статистическая вероятность наступления страхового случая, которая подразумевает, что из некоторого количества объектов страхования только отдельные подвергаются страховому случаю. Согласно теории вероятностей вероятность события А, которую обозначают Р(А), определяют как отношение числа элементарных исходов М, благоприятствующих событию А, к их общему числу N:

P(A) = M/N

Так как вероятность выражается правильной дробью, в которой числитель меньше знаменателя, то М всегда меньше или в пределе равно N. При этом вероятность события А можно выразить в следующем виде:

0 ≥ Р(А) ≤ 1

Отсюда следует, что событие А считается невозможным, если Р(А) равно 0. Если же Р(А) равно 1, то это событие считается достоверным, состоявшимся. При достижении вероятности крайних значений (0 или 1) страхование на случай наступления данного события проводиться не может.

В качестве примера произведем расчет на 100 застрахованных объектов. Предположим, что статистика страхования показывает: ежегодно 2 объекта из этого числа подвергаются страховому случаю. Оценим вероятность того, что в текущем году с любым из 100 застрахованных объектов произойдет страховой случай по формуле (1). Вероятность наступления страхового случая будет равна 0,02 или 2 %. Предположим, что в нашем примере каждый объект застрахован на страховую сумму в 300 рублей. При этом мы помним о том, что страховая сумма является максимальной суммой страховой выплаты за один объект. В имущественном страховании страховой суммой является действительная стоимость имущества, в страховании жизни – денежная сумма, которую назначает по своему желанию страхователь. Если бы каждый объект в нашем примере был застрахован на 300 рублей, то ежегодные страховые выплаты составили бы: 0,02 х 100 х 300 = 600 рублей (здесь: 0,02 – вероятность страхового случая, 100 – число застрахованных объектов, 300 – сумма страховой выплаты за один объект). Разделив вероятностную выплату на число застрахованных объектов, получим долю одного страхователя в страховом фонде. В нашем примере эта доля равна 6 рублей (600:100= 6 руб.). Именно такой страховой взнос (страховую премию) должен уплатить каждый страхователь при страховой сумме 300 рублей, чтобы компания имела достаточно средств для выплаты страхового возмещения. Если пересчитать нетто-ставку на единицу страховой суммы, то она будет равняться 2 рубля со 100 рублей страховой суммы: 0,02 х 100 = 2 руб.

Нетто-ставка, как видно из примера, отражает степень риска страховщика по данному договору страхования. Нетто-ставка – это часть страхового тарифа, связанная с формированием фонда выплат страхового возмещения. При расчете тарифов страховщик обычно решает трудную задачу: при минимальном страховом тарифе обеспечить максимальный объём страховой ответственности.

Поскольку нетто-ставка рассчитывается на основании статистической вероятности наступления страхового случая для некоторого количества объектов (100 застрахованных объектов – в нашем примере), на практике нетто-ставка корректируется на поправочный коэффициент Кn. Коэффициент Кn равен отношению средней величины страховой выплаты к средней величине страховой суммы на один договор: К n= С в: С с, где С в– средняя величина выплаты на один договор; С с– средняя величина страховой суммы на один договор. Затем по формуле, определяющей «вероятность ущерба», рассчитывают нетто-ставку со 100 денежных единиц (д.е.) страховой суммы:

Т nс= Р(А) х К n* 100 д.е., (2)

где К nс– тарифная нетто-ставка;

Р(А) – вероятность наступления страхового случая А;

К n– поправочный коэффициент.

Данную формулу используют в следующих случаях:

– при совершенствовании тарифных ставок по действующим видам страхования;

– при расчете ставок по вновь вводимым страховым услугам.

Представим формулу в развернутом виде

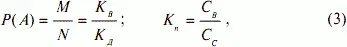
где К в– количество выплат за то или иной период (обычно за год);