Анатолий Квашин - Пара слов

59. Назовем этот узел – Узлом Вселенной.

60. Говоря о себе: “я есмь”, я помещаю себя в Узел Вселенной».

Стоит заметить, что помещение себя в «Узел Вселенной» связано у Хармса с действием говорения, речи, причем сама фраза «я есмь» вызывает конкретные библейские ассоциации. Таким образом, мы можем предполагать, что именно слово есть то препятствие, – может быть, та материя, – которое образует существование.

Также с «троицей существования» вполне соотносится таблица из тетради «Существование», оглашенная А.Александровым на конференции "ОБЭРИУ и театр" в 1990 году 19 19 Таблица приводится по: Кацис Л. Ф. Пролегомены к теологии ОБЭРИУ (Даниил Хармс и Александр Введенский в контексте Завета Св. Духа) // Кацис Л. Русская эсхатология и русская литература. – М., 2000. – с. 467-488. .

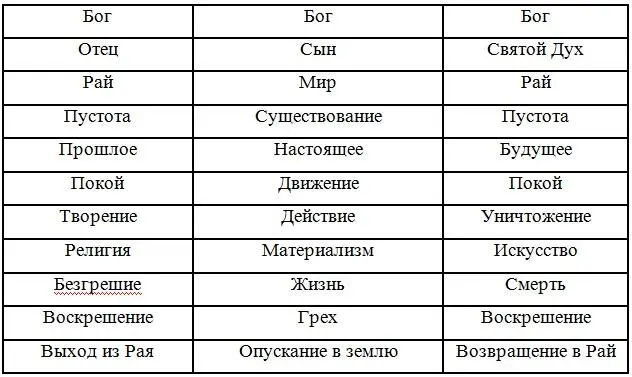
Данная таблица уже неоднократно описывалась и интерпретировалась исследователями. Л.Ф. Кацис пишет о том, что в таблице (при вертикальном ее прочтении) представлено три «завета»: Завет Бога-Отца, Завет Бога-Сына и Завет Бога-Святого Духа. Особенно интересна третья колонка – Завет Святого Духа, в котором искусство становится в ряд с исчезновением, пустотой, будущим, покоем, разрушением, уничтожением, воскрешением, смертью и возвращением в рай. Категории, с рациональной точки зрения, понимаемые как отрицательные (разрушение, уничтожение, смерть), входят в положительный ряд рая-будущего с его покоем и воскрешением 20 20 Гладких Н.В. Проза Даниила Хармса: Вопросы эстетики и поэтики. . При горизонтальном же прочтении таблицу можно прочесть как более подробно расписанную «троицу существования» (препятствием в данном случае становится средний столбец мир-настоящее , разделяющий рай-прошлое и рай-будущее ).

Кроме того, идею препятствия Хармс развивает в трактате «О кресте». Графически изображая небытие (т.е. «нечто единое, однородное и непрерывное») в виде прямой линии, поэт представляет препятствие перпендикуляром, разрезающим эту прямую. Превращая это графическое изображение в символическую фигуру, Хармс получает крест, который называет символом существования. С фигурой креста в философии Д.И. Хармса тесно связаны понятия ноля – круга, к которым мы сейчас и обратимся.

б) Ноль и нуль. Круг

Теперь же перейдем к рассмотрению трактатов «Нуль и ноль» и «О круге» (оба – 1931г.). У Хармса особое отношение к числам (особенно в ряду от 1 до 8). Каждое из чисел рассматривается им как самостоятельная сущность, прямо не связанная с его местом в счетном ряду 21 21 Гладких Н.В. Проза Даниила Хармса: Вопросы эстетики и поэтики. . Так в трактате «Нуль и ноль» Хармс пишет: «Понятие “больше” и “меньше” столь же недействительно как понятие “выше” и “ниже”. Это наше частное условие считать одно число больше другого и по этому признаку мы расположили числа, создав солярный ряд. Не числа выдуманы нами, а их порядок. Многим покажется, что существо числа всецело зависит от его положения, что число может быть рассматриваемо самостоятельно, вне порядка ряда. И только это будет подлинной наукой о числе». Той же мыслью начинается неозаглавленная запись, опубликованная в том же номере «Логоса»: «Числа не связаны порядком. Каждое число не предполагает себя в окружении других чисел».

Особо выделяется Хармсом ноль , противопоставляемый нулю 22 22 М.Б. Ямпольский считает, что в стихотворении "Третья цисфинитная логика бесконечного небытия" (1930) через оппозицию букв "о" и "у" воспроизводится (хотя и в скрытой форме) оппозиция нуля и ноля. (Ямпольский М. Б. Беспамятство как исток (Читая Хармса). – М., 1998. – с. 306-307). , который, как мы уже говорили, является обозначением несуществования: «Предполагаю и даже беру на себя смелость утверждать, что учение о бесконечном будет учением о ноле. Я называю нолем, в отличие от нуля, именно то, что я под этим и подразумеваю» («Нуль и ноль»). То же противопоставление прослеживается в дневниковой записи от 19 сентября 1933 года: «Числа в своем нисхождении не оканчиваются нулем. Но система отрицательных количеств – вымышленная система. Я предполагал создать числа меньше нуля – Cisfinitum. Но это тоже было неверно. Нуль заключает в себе самом эти неизвестные нам числа. Может быть, правильно было бы считать эти числа как некие нулевые категории. Таким образом, нисходящий ряд чисел принял бы такой вид: