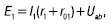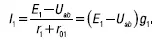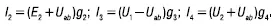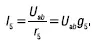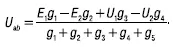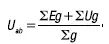Юлия Щербакова - Электроника и электротехника. Шпаргалка

В зависимости от значений и направлений ЭДС и напряжений, а также значений сопротивлений ветвей между узловыми точками а и b установится определенное узловое напряжение Uab . Предположим, что оно направлено так, как показано на рисунке 12, и известно. Зная напряжение Uab , легко найти все токи.

Выберем положительные направления токов, например так, как показано на рисунке. Тогда по второму закону Кирхгофа для контура, проходящего по первой ветви,

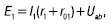
откуда:

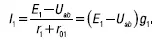
Поступая аналогичным способом, нетрудно получить формулы для токов I 2, I 3 и I 4:

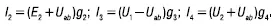
По закону Ома для пятой ветви:

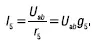
Для вывода формулы, позволяющей определить напряжение Uab . Преобразуем формулу по первому акону Кирхгофа:

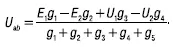
Формула узлового напряжения в общем случае имеет вид:

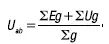
Перед определением напряжения по последней формуле следует задаться его положительным направлением. Со знаком «+» должны входить ЭДС, направленные между точками а и b встречно напряжению Uab , и напряжения ветвей, направленные согласно с Uab . Знаки в последней формуле не зависят от направления токов и ветвей.

При анализе и расчете электрических цепей методом узлового напряжения целесообразно выбирать положительные направления токов после определения узлового напряжения. В этом случае положительные направления токов нетрудно выбрать таким образом, чтобы все они совпадали с их действительными направлениями.

Метод наложенияоснован на том, что в линейных электрических цепях ток любой ветви может быть определен как алгебраическая сумма токов от каждого источника в отдельности.

Расчет электрических цепей методом наложения производят в таком порядке. Из электрической цепи удаляют все источники ЭДС и напряжения, кроме одного. Сохранив в электрической цепи все резистивные элементы, в том числе и внутренние сопротивления источников, производят расчет электрической цепи. Внутренние сопротивления источников с указанными напряжениями полагают равными нулю.

Подобным образом поступают столько раз, сколько имеется в цепи источников.

Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников.

Для того чтобы результирующие токи совпадали с действительными направлениями, целесообразно выбирать положительные направления результирующих токов после определения токов от всех источников.

Метод наложениявесьма удобен для анализа явлений, происходящих в электрических цепях при изменении их параметров.

Например, используя метод наложения, нетрудно определить характер изменения токов ветвей в цепи (см. рис. 13) при увеличении ЭДС E 1 до E 1′ .

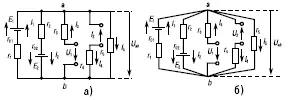
Рис. 13. Схема электрической цепи

Действительно, предположим, что при некоторых параметрах цепи до увеличения E 1 установились токи, действительные направления которых совпадают с указанными на рисунке 13. Для решения задачи заменим мысленно увеличение ЭДС E 1 введением в первую ветвь дополнительного источника с r 0доп = 0 и Е доп = E 1′ – E 1. После этого удалим из цепи все источники, кроме источника с ЭДС Е доп, и определим действительные направления дополнительных токов от этого источника, которые очевидны.

Поскольку дополнительный ток первой ветви I 1доп будет совпадать по направлению с током I 1, для определения результирующего тока первой ветви следует воспользоваться формулой I 1′ = I 1 + I 1доп. На основании данной формулы можно сделать вывод о том, что при увеличении Е 1 ток I 1 будет возрастать.

К такому же выводу можно прийти и в отношении токов других ветвей, кроме третьей.

Так как дополнительный ток третьей ветви I 3доп направлен против тока I 3, то для определения результирующего тока нужно использовать формулу I 3′ = I 3 + I 3доп. В отношении результирующего тока третьей ветви можно сделать такой вывод: при увеличении ЭДС Е 1 ток I 3 будет сначала уменьшаться, при некотором значении Е 1 окажется равным нулю, а при дальнейшем увеличении Е 1 изменит направление ( I 3 < 0) и по абсолютному значению будет возрастать.