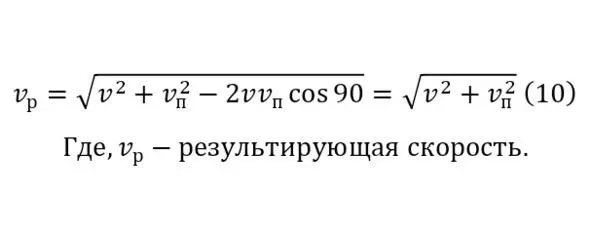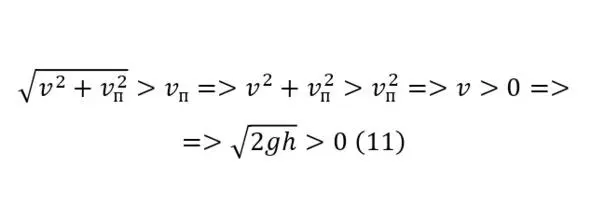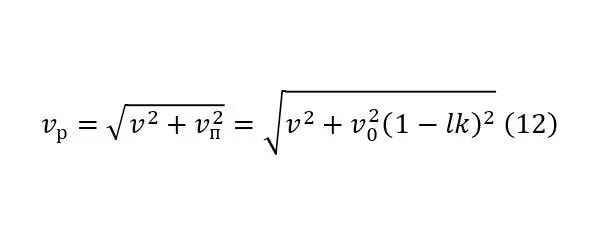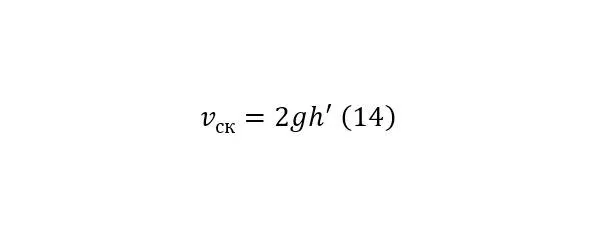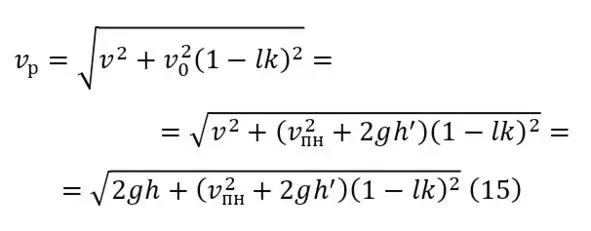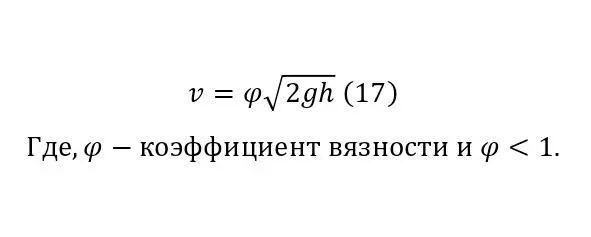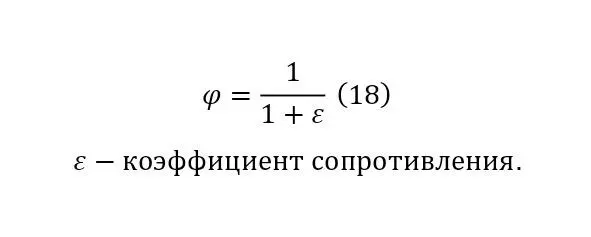Екатерина Вавилова - Все науки. №6, 2022. Международный научный журнал

Данный вектор скорости суммируется с образующимся вектором скорости из-за давления (8) под прямым углом образуя результирующий вектор (10).

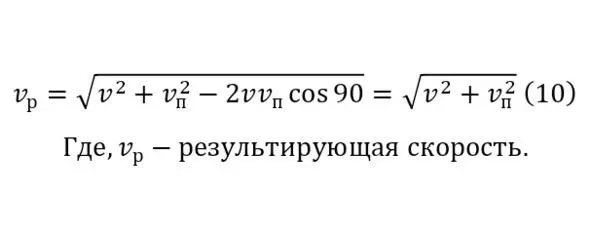
Выводимый результирующий вектор логично будет больше изначального вектора скорости (11), благодаря чему можно сделать вывод того, что использование плотин в конструировании малых гидроэнергетических установок вполне целесообразная технология.

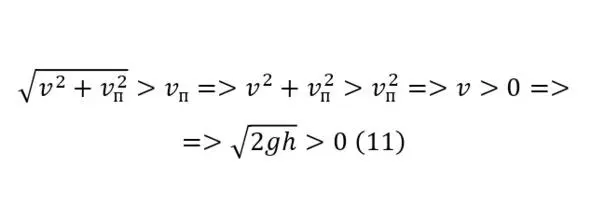
То есть какой бы ни была малой высота плотины и её разность между отверстием вывода потока и уровнем воды, действие, хоть и незначительное будет оказываться. Интересно здесь также и определение зависимости самой изначальной скорости и результирующего вектора (12).

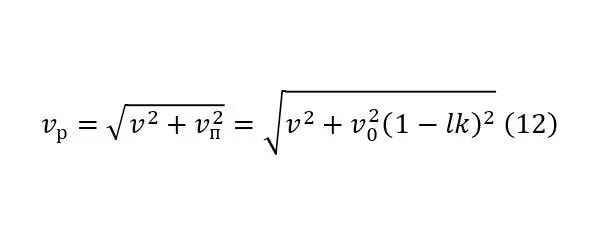
Эта зависимость была выведена, поскольку даже сама начальная скорость не совсем проста и за счёт того, что нижняя полость оврага для «водохранилища» должна быть выполнена в форме склона. Наряду с уменьшением по коэффициенту в зависимости от длины этого пути по (9), начальная скорость будет увеличиваться, поскольку к первоначальной скорости до входа в «водохранилище», при котором поток имел потенциальную энергию, кинетическая энергия, в которую превращается эта потенциальная, то есть действует тот же принцип (1—5), но при этом действует угловой коэффициент.

И если поскольку опять же этот потенциальный вектор направляющий вниз также находится под углом 90 градусов к основному первоначальному вектору, их суммированных вектор будет определяться по (13), создавая зависимость для начальной скорости от первоначальной в следующем расположении.

Откуда справедливо (14).

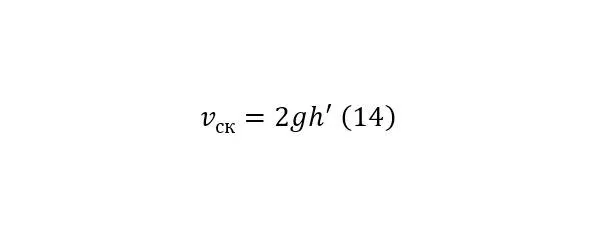
И важно учесть, что (13) вместе с (14) действует только при плоском склоне самого оврага, не считая коэффициент трения, в случае его расчёта в (14) включается дополнительный коэффициент, ровно, как и в иных случаях, для реализации, но этот коэффициент определяется эмпирически.

При действии же (13) и (14), ранее описанная (12) изменяется как (15).

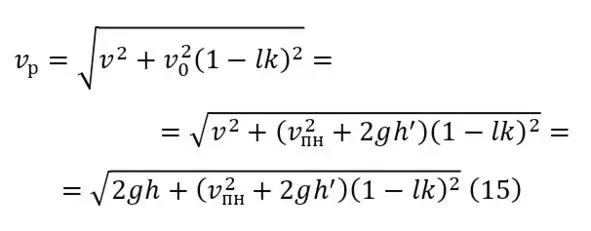
Таким образом (15) можно считать полноценной формулой при действии прямого склона на дне оврага. При наличии же нескольких векторов, целесообразно использование (16), по той простой причине, что несколько векторов не будут приходить из одного направления, ибо тогда их можно будет объединить в один. А разными вектора могут быть из-за наличия дополнительных поворотов, больших неровностей и подобных не существенных причин.

Заключительным штрихом служит лишь введение коэффициентов, о которых говорилось ранее, а именно о коэффициентах своего рода вязкости (18), зависящий от коэффициента сопротивления движения в потоке (17).

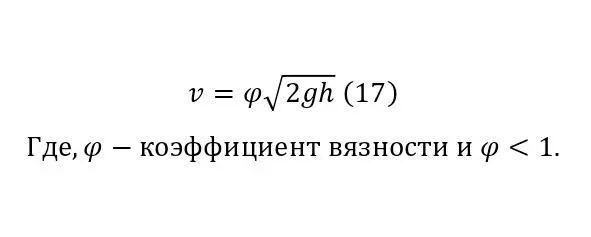
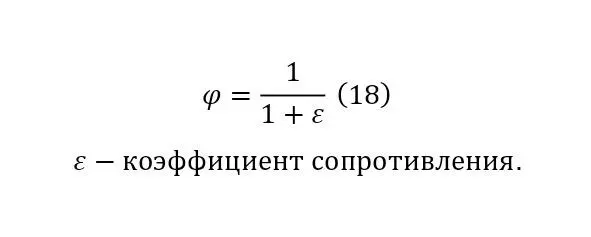
Такой вид (17) формулы (8) был доказан и описан итальянским учёным Эванджелиста Торричелли в 1643 году, а позже уже было показано, что эта формула, как уже упоминалось следствие закона Бернулли.

В заключении можно отметить, что развитие гидроэнергетики несёт в себе весьма прогрессирующий характер, что радует. И данное развитие требует всё новых и новых технологий, среди которых одним из лучших может стать технология использования «малого водохранилища» или искусственного рва с наклонным дном для увеличения эффективности всей гидроэнергетической установки.