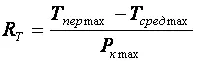τ н = C р ( R Л + R П ),
где R Л — эквивалентное сопротивление, стоящее слева от C р (обычно это выходное сопротивление предыдущего каскада или внутреннее сопротивление источника сигнала), R П — эквивалентное сопротивление, стоящее справа от C р (обычно это входное сопротивление следующего каскада или сопротивление нагрузки).
Для рассматриваемой цепи постоянная времени равна:
τ н 2= C р 2( R к + R н ).
Выражения для относительного коэффициента передачи и коэффициента частотных искажений в области НЧ таковы:
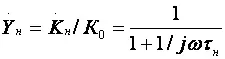
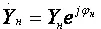
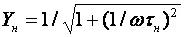
φ н= –arctg ωτ н,
M н = 1/ Y вн
и в комментариях не нуждаются. По этим выражениям оценивается влияние конкретной цепи на АЧХ и ФЧХ каскада в области НЧ.
Связь между коэффициентом частотных искажений и нижней граничной частотой выражается формулой

Аналогичным образом учитывается влияние других разделительных и блокировочных цепей, только для блокировочной эмиттерной цепи постоянная времени приблизительно оценивается величиной τ нэ≈C э/ S 0 т.к. сопротивление БТ со стороны эмиттера приблизительно равно 1/ S 0 (см. подраздел 2.4.1), а влиянием R э в большинстве случаев можно пренебречь, т.к. обычно 1/ S 0<< R э .
Результирующую АЧХ и ФЧХ каскада в области НЧ можно построить, используя уже упоминавшийся принцип суперпозиции.
В n-каскадном усилителе с одинаковыми каскадами наблюдается эффект сужения полосы рабочих частот, который в области НЧ можно скомпенсировать уменьшением нижней граничной частоты каскадов до 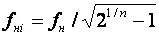 .
.
2.6. Термостабилизация режима каскада на биполярном транзисторе
Параметры БТ в значительной мере подвержены влиянию внешних факторов (температуры, радиации и др.). В то же время, одним из основных параметров усилительного каскада является его стабильность. Прежде всего, важно, чтобы в усилителе обеспечивался стабильный режим покоя.
Проанализируем вопрос влияния температуры на стабильность режима покоя БТ, конкретно — I к 0.
Существуют три основных фактора, влияющих на изменении I к 0 под действием температуры: при увеличении температуры, во-первых, увеличивается напряжение U бэ 0, во-вторых, обратный ток коллекторного перехода I кбо , и, в третьих, возрастает коэффициент H 21э.
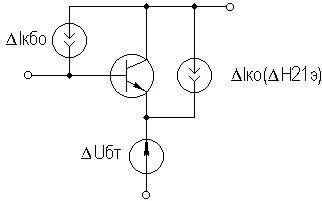
Рисунок 2.16. Тепловая модель БТ
Для анализа реальный транзистор можно представить в виде идеального, у которого параметры не зависят от температуры, а температурную зависимость смоделировать включением внешних источников напряжения и тока (рисунок 2.16).
Рассмотрим влияние этих факторов на приращение тока коллектора Δ I к 0. Начнем с влияния изменения U бэ 0, вызванного тепловым смещением проходных характеристик I к = f ( U бэ ), обозначив при этом приращение тока коллектора как Δ I к 01:
Δ I к 01= S 0·Δ U бТ ,
где Δ U бТ — приращение напряжения U бэ 0, равное:
Δ U бТ = |ε T |·Δ Т ,
где ε T — температурный коэффициент напряжения (ТКН),
ε T ≈ –3мВ/град., Δ Т — разность между температурой коллекторного перехода перехода T пер и справочным значением этой температуры T спр (обычно 25°C):
Δ Т = T пер– T спр ,
T пер= T сред+ P кR T ,
где P к и R T соответственно, мощность, рассеиваемая на коллекторном переходе в статическом режиме, и тепловое сопротивление “переход-среда”:
P к = I к 0· U к 0,
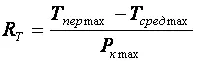
Ориентировочное значение теплового сопротивления зависит от конструкции корпуса транзистора и обычно для транзисторов малой и средней мощности лежит в следующих пределах:
R T = (0,1…0,5) град./мВт.
Читать дальше

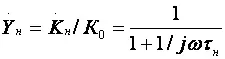
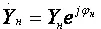
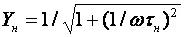

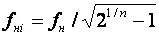 .
.