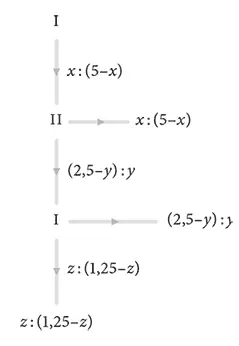Юн Эльстер - Объяснение социального поведения. Еще раз об основах социальных наук

В игре «Ультиматум» (рис. XIX.5) и других последовательных играх равновесие находят в обратной индукции. В игре «Ультиматум» Предлагающий предвосхищает реакцию Респондента на его предложение и приспосабливает к ней свое поведение. Сопутствующие этим примерам расчеты очень просты. В других экспериментах от участников могут потребоваться более сложные цепочки рассуждений. Например, двое из них проходят три раунда предложений и встречных предложений, чтобы поделить сумму денег, которая в каждом следующем раунде уменьшается на 50 % [266]. Каждый раз агент может либо принять предложение и пойти напрямую, либо сделать встречное предложение и снизить ставки. Рациональность, эгоистический интерес и общеизвестность приведут его к следующему рассуждению.

Человек, делающий первое предложение (игрок 1), должен будет учесть, предпочтет ли игрок 2 данное разделение такому, при котором он получит больший кусок от меньшего пирога. В то же время игрок 1 знает, что игрок 2 не сделает предложения, от принятия которого игроку 1 будет хуже, чем если бы он перешел к последнему раунду. На рис. XX.2 игрок 1 может получить по меньшей мере 1,25, забрав все, что осталось в третьем раунде. Таким образом, игрок 2 не может предложить ему менее 1,25 во втором раунде, оставив максимум 1,25 для себя. Зная об этом, игрок 1 предложит (3,75: 1,25), и игрок 2 примет предложение.

В экспериментах среднее предложение, сделанное игроком 1, составляет (2,89: 2,11), что значительно щедрее равновесного варианта. Очевидно, что нарушается одно или даже несколько допущений. (1) Первый игрок может быть альтруистом. (2) Он может опасаться, что другой игрок отвергнет равновесное предложение, потому что не способен понять логику обратной индукции. (3) Он сам не способен понять эту логику [267]. Первая и вторая гипотезы могут быть устранены, если сказать игрокам, что они играют с компьютером, запрограммированным на оптимальный ответ. В этом случае первое среднее предложение составляет (3,16: 1,84), то есть по-прежнему значительно больше равновесного. Поскольку участники, делающие щедрые предложения, едва ли могут испытывать альтруистические чувства к компьютеру или считать его некомпетентным, по-видимому, некомпетентны они сами.

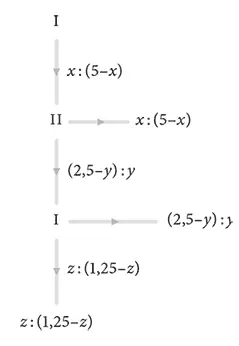
РИС. XX.2

Проблема не в том, что это трудная задача. Как только участникам объясняют логику обратной индукции, в последующих играх они все проделывают безукоризненно. Скорее эксперимент показывает, что такого рода рассуждения людям несвойственны. Даже обычная предусмотрительность не всегда возникает спонтанно, как показывает проклятие победителя (глава XII). Нечто подобное есть и в синдроме младшего брата (глава XVIII). Не то чтобы люди, поразмыслив, не могли понять, что другие так же рациональны и способны к оценке последствий, как и они, просто у них есть стихийная склонность полагать, что другие сильнее укоренены в своих привычках и не способны приспосабливаться к обстоятельствам.

Из множества примеров неудач в предсказаниях, сделанных теорией игр, я хочу остановиться на «Дилемме заключенного» с конечным числом повторений, «парадоксе сетевого магазина», играх «Сороконожка», «Дилемма путешественника» и «Конкурс красоты».

Когда участники многократно играют друг с другом в «Дилемму заключенного» и знают, какой раунд будет последним, мы наблюдаем значительную долю выбора С , иногда превышающую 30 %. Интуитивно можно предположить, что игрок выберет С в одном раунде в надежде на то, что другой ответит ему взаимностью (услуга за услугу). Но если игроки применят обратную индукцию, то поймут, что в финале оба выберут D , поскольку в более поздней игре нет возможности влиять на поведение. В предпоследней игре игроки также выберут D , поскольку поведение в финале задается предшествующим рассуждением. Этот аргумент «отыгрывается назад» вплоть до первого раунда, мотивируя отказ от сотрудничества во всех играх.

Сетевой магазин имеет филиалы в 20 городах и в каждом из них сталкивается с потенциальным конкурентом. Конкурент должен решить: открывать ли магазин, чтобы разделить рынок с сетевым игроком, или отказаться от ведения дел в этом городе. Сетевой магазин имеет возможность отреагировать агрессивно, резко снизив цены, тем самым он разорит соперника, но и сам понесет убытки. Или же он может согласиться на раздел рынка. Выигрыши представлены на рис. XX.3; первое число в каждой паре – выигрыш для потенциального конкурента.