Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Л. — Противоречивость требований делает задачу весьма неприятной, но тем не менее путем соответствующего компромисса можно найти приемлемое решение. Для достижения максимального снижения вносимых погрешностей следует поставить на место R 2 потенциометр сопротивлением 14 000 ом. Однако при желании перемножать три величины с помощью трех каскадно соединенных потенциометров исключительно трудно подобрать потенциометры с возрастающими в геометрической прогрессии сопротивлениями. Поэтому в таких случаях мы воспользуемся более простым способом: между движком потенциометра R 1 и резистивной обмоткой потенциометра R 2 мы поместим усилитель, понижающий сопротивление, с коэффициентом передачи как можно ближе к единице и обладающим высоким входным и низким выходным сопротивлениями.

Н. — Я полагаю, что здесь ты используешь что-нибудь вроде эмиттерного повторителя или своего суперэмиттериого повторителя, схему которого ты изобразил для меня на рис. 50.

Л. — Совершенно верно. И раз мы уже начали говорить об аналоговой вычислительной технике, я покажу тебе, какой интерес могут представлять операционные усилители.

Н. — Вот новая категория усилителей, о которой я ничего не знаю!

Л. — И их ты знаешь значительно больше, чем думаешь. Дело в том, что так называют усилители с непосредственной связью, обладающие высоким коэффициентом усиления, очень высоким входным сопротивлением и очень низким выходным сопротивлением. Несколько позже мы рассмотрим, как такие усилители делают.

А теперь представь себе, что мы собрали усилитель по схеме, приведенной на рис. 151.

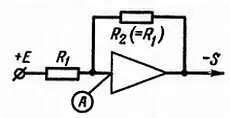
Рис. 151. Из-за глубокой отрицательной обратной связи коэффициент передачи усилителя становится равным — 1 (при этом следует считать, что напряжение в точке Апочти равно нулю и что входной ток усилителя тоже ничтожно мал).

Усилитель имеет отрицательный коэффициент передачи; иначе говоря, он имеет на выходе отрицательное напряжение, когда на его вход подается положительное напряжение (очень небольшое, потому что коэффициент усиления имеет очень большую величину). Можешь ли ты сказать, какой ток протекает по резисторам R 1 и R 2 , имеющим одинаковое сопротивление?

Н. — Ты так подчеркивал очень большое значение коэффициента усиления, что я предполагаю, что потенциал на входе А следует считать равным нулю. Тогда протекающий по резистору R 1 ток будет A / R 1 , а ток, протекающий по резистору R 2 , будет A / R 2 .

Л. — Совершенно верно. А теперь скажи, пожалуйста, как относятся значения этих токов один к другому?

Н. — Не имею ни малейшего представления.

Л. — А ведь я тебе сказал, что входное сопротивление этого усилителя очень высокое. Следовательно, его входной ток практически равен нулю. Это означает, что протекающие по резисторам R 1 и R 2 токи равны между собой. А если резисторы R 1 и R 2 имеют одинаковое сопротивление, ты можешь сделать вывод, что Е = S .

Н. — Ты изрядно потрудился, чтобы еще раз дать мне объяснение отрицательной обратной связи.

Л. — Я очень рад, что ты ее узнал. Как ты видишь, такой усилитель позволяет произвести инверсию, т. е. получить для имеющегося напряжения равное ему, но с обратным знаком. Если в этих условиях сопротивление резистора R 2 не было равно сопротивлению резистора R 1 , а было бы, например, в 5 раз больше его, то выходное напряжение стало бы в 5 раз больше входного; иначе говоря, мы можем получить удобное средство для умножения напряжения на 5.

Н. — Но все это в свое время ты мне уже объяснял, и я не вижу ничего нового.

Л. — К этому мы сейчас подойдем. А теперь рассмотрим схему, приведенную на рис. 152.

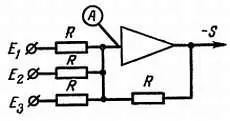
Рис. 152. Эта схема дает выходное напряжение, по абсолютной величине равное (но с противоположным знаком) сумме трех входных напряжений.

Токи, протекающие по трем расположенным слева резисторам, соответственно равны E 1 / R, E 2 / R и E 3 / R . Ток, протекающий по расположенному справа резистору, равен, как мы только что установили, S / R . Потенциал точки А из-за очень высокого коэффициента усиления усилителя следует, как и раньше, считать равным нулю. Из-за высокого входного сопротивления поступающий на вход усилителя ток следует также рассматривать как равный нулю. Это означает, что сумма трех поступающих в точку А токов должна быть равна выходному току. Если при написании этого равенства из всех его членов убрать знаменатель R , то мы получим Е 1 + Е 2 + Е 3 = S . Таким образом, мы получили напряжение, равное сумме трех напряжений.