Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Л. — Твой механический счетчик проще по устройству, а его показания легче прочитать. Но я повторяю, что при удачном выборе первых триггеров в цепочке мы можем считать импульсы, следующие со скоростью нескольких миллионов и даже нескольких десятков миллионов в 1 сек.

Н. — Об этом я не думал, но тогда потребуется действительно солидное количество каскадов, иначе возможности твоего счетчика быстро окажутся недостаточными.

Л. — С этим доводом нельзя не согласиться, так как способный считать до миллиона счетчик должен иметь 20 каскадов. Но я напоминаю тебе, что эти каскады, особенно работающие в невысоком ритме, относительно просты. И я полностью согласен с тобой, что такой бинарный счетчик (работающий в бинарной системе счисления, признающей только две цифры — нуль и единицу) не очень удобен в работе. Поэтому разработали более совершенные счетчики, позволяющие считать в нашей привычной десятичной системе.

Н. — Можешь ли ты описать мне один из них… Я боюсь, как бы он не оказался ужасно сложным.

Л. — Некоторые из этих схем достаточно сложны. Мы рассмотрим только одну так называемую счетную декаду, представляющую собой электронную схему, которая по получении десяти импульсов всегда возвращается в первоначальное состояние. По получении десятого импульса она дает в канал, именуемый выходом, импульс, приводящий в действие следующую декаду.

Я покажу тебе устройство декады, разработанной инженерами фирмы Rochar , структурная схема которой изображена на рис. 117. Как ты видишь, в начале схемы стоит первый триггер с двумя устойчивыми состояниями, который я вновь изобразил в виде прямоугольника (на этот раз триггер опять собран по схеме на рис. 82).

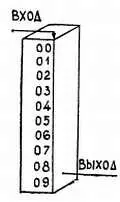
Рис. 117. Структурная схема счетной декады, выпускаемой французской фирмой Rochar. Схема В 1с двумя устойчивыми состояниями является делителем на 2; устройство, состоящее из трех других триггеров, последовательно проходит пять возможных состояний.

Н. — Ты опять нарисовал два входа, но это не нужно, потому что ты всегда соединяешь их вместе.

Л. — Нет, не всегда. Я могу подавать на них разные сигналы, например сигналы одного типа на конденсатор С 3 и другого типа на С 4 . По этой причине я и рассматриваю триггер как схему с двумя входами. Когда триггер используют в качестве делителя частоты на 2, входы соединяют вместе и одновременно подают на них отрицательные импульсы. Мы назвали нулевым состоянием (или состоянием покоя) положение, когда транзистор Т 1 пропускает ток, а транзистор Т 2 заперт. Когда триггер возвращается на нуль, резкое снижение потенциала коллектора транзистора Т 1 посылает через дифференцирующую схему (из которой я изобразил здесь только конденсатор) отрицательный импульс. Поэтому, как ты видишь, на каждый второй поступивший на вход импульс в точку В приходит отрицательный импульс.

Н. — Да, и я также вижу, что этот импульс затем идет по двум направлениям: во-первых, на триггер В 2 , куда он странно поступает только на один вход, а, во-вторых, на схему, обозначенную на рисунке буквой G, о которой я ровным счетом ничего не могу сказать.

Л. — Попробуем рассуждать по порядку. В самом деле, сигнал в триггер В 2 поступает только на базу его транзистора Т 1 . От первого импульса, попавшего на его левый вход, триггер опрокинется и с нуля перейдет на единицу ( Т 1 заперт, Т 2 в состоянии насыщения). Последующие отрицательные импульсы, которые могут поступить из точки В , не окажут на него никакого воздействия до тех пор, пока он не будет возвращен на нуль.

Схему, обозначенную на рисунке буквой G , называют ключевой; управляемый напряжением электронный ключ не пропускает в точку F импульсы, подаваемые на его левый вход, если напряжение на его входе D равно нулю. Если же на вход D поступает положительное напряжение, то ключ откроется для прохода импульсов и приходящие на его левый вход импульсы окажутся в точке F .