Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

Но врач мог принять за основную гипотезу наличие у больного инфаркта миокарда. В этом случае возможны также два исхода: диагноз подтвердился и диагноз ошибочный. Причем ошибка, увы, также может стоить человеку жизни. Всю описанную ситуацию можно представить в виде таблицы:

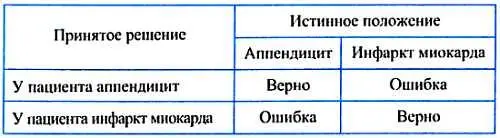
Конечно, врач не имеет права гадать. Поэтому он назначит дополнительное обследование: снимет электрокардиограмму, возьмет определенные анализы и, когда результатов обследования окажется достаточно, примет окончательное решение. Правда, и в данном случае врач не застрахован от ошибки. Но почему же, однако, в большинстве случаев больным ставится верный диагноз и назначается правильное лечение? Это происходит оттого, что, принимая решение, врач руководствуется статистическими данными, накопленными медициной в большом количестве. Без этого богатейшего опыта здравоохранение вряд ли добилось бы каких-либо успехов.

В житейских ситуациях мы также опираемся на статистику, хотя не всегда осознаем это. Скажем, если ваш приятель, повстречавшийся вам в ясный морозный день, с восторгом рассказывает, как он только что провел отпуск, ни разу не надев пальто, вы уверенно делаете вывод, что отдыхал он уж, конечно, не в Сибири, а на юге. Такая уверенность основана на том, что внезапное потепление в Сибири, хотя, в принципе, и возможно, но в такое время года и на столь длительный период (на время отпуска) маловероятно. В то же время для южных районов страны теплая погода является нормой.

Нам кажется, что пример из медицинской диагностики поможет лучше уяснить ситуацию, сложившуюся в цифровой системе передачи. На приемной станции нужно ставить "диагноз" каждому "израненному" помехой импульсу, т. е. необходимо принимать решение о том, что передается в каждый данный промежуток времени: 0 или 1. Все возможные варианты, возникающие при этом, сведены в таблицу:

Заметим, что подобные задачи возникают не так уж редко. В системе противовоздушной обороны есть радиолокационная служба обнаружения. Она тоже не безошибочна: сигнал о вражеском объекте может быть принят за шум, либо может быть сделано ошибочное заключение об обнаружении объекта, когда его на самом деле нет. Как пропуск жизненно важной информации, так и ложная тревога чреваты в наши дни самыми трагичными последствиями для миллионов людей. Этими примерами мы хотим подчеркнуть, насколько важно принять правильное решение.

- Но ошибки в приеме цифровой информации не угрожают жизни людей, - заметит читатель. - Не сгущают ли авторы краски?

Это как посмотреть. Если речь идет о светской болтовне двух приятельниц, то здесь читатель безусловно прав: частые ошибки при приеме цифровой информации вызовут лишь законное возмущение приятельниц качеством связи. Однако цифровая информация может передаваться, скажем, от центра управления полетом к стартовому ракетному комплексу, от высшего военного руководства к командному пункту войск ПВО, от переносного электрокардиографа к приемному комплексу в поликлинике. Да мало ли какая жизненно важная информация может содержаться в цифровом потоке! Тут уж, перефразируя известное изречение, искажение смерти подобно. Другое дело, что в разных ситуациях можно допустить разную степень "ошибочности" при принятии решения.

В самом деле, как оценивать качество "диагностики" пораженных помехами импульсов? Самый простой способ - подсчитывать количество ошибочно принятых решений. Но так как абсолютное число ошибок не дает представления о качестве "диагностики", разумно отнести его к общему числу переданных импульсов. Например, если из тысячи импульсов приняты неверно три, то отношение количества ошибочно принятых решений к общему числу решений составит 0,003, или 3∙10 -3. В математике это отношение принято называть вероятностью ошибок. Чем она меньше, тем качественнее осуществляется "диагностика" импульсов.

Как же узнают о том, что принятое решение ошибочно? - удивится читатель. - Ведь на приеме неизвестно, какой символ передавался, а если бы это было известно, то зачем тогда такую информацию передавать? В данном случае связь не нужна. Конечно, мы не знаем, верно или неверно принят тот или иной символ. Но существует удивительная математическая наука - теория вероятностей. Она позволяет еще на стадии проектирования, т. е. когда цифровой системы передачи даже и в помине нет, рассчитать вероятность ошибочного приема или, иными словами, узнать, сколько раз в среднем мы ошибемся.