Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

Еще не так давно был распространен счет по дюжинам (т. е. число 12), дюжинам дюжин — "гроссам", дюжинам гроссов — "массам" для белья, посуды, писчебумажных товаров. Дома у нас сервизы содержат по 12 чашек, 12 блюдец, 12 тарелок.

О широком распространении двенадцатеричной системы свидетельствуют такие факты: мы до сих пор делим год на 12 месяцев; у англичан в системе мер 1 фут равен 12 дюймам, а в денежной системе 1 шиллинг равен 12 пенсам. Число 12 часто встречается также в сказках и легендах (12-главый змей, 12 братьев-разбойников), что говорит о древнем происхождении этой системы счисления.

Посмотрим, как будет представлено в ней число 777. Поскольку в системе должно быть двенадцать цифр, а мы знаем только десять, то придется ввести еще две цифры, обозначив 10, скажем, буквой А, а 11 — буквой Б. Осуществив последовательное деление нашего числа на основание 12, получим

(777) 10= 5∙12 2+ 4∙12 + 9= ( 549) 12

Число (35) 10=2∙12 + 11 запишется как (2Б) 12, а число (134) 10= 11∙12 + 2 - как (Б2) 12, т. е. оно станет двузначным.

Как видите, можно придумать много различных позиционных систем счисления, отличающихся только основаниями. И вес они, вообще говоря, равнозначны: ни одна из них не имеет явных преимуществ перед другой! Так почему же все-таки мы пользуемся именно десятичной системой счисления?

Вряд ли можно дать на этот вопрос исчерпывающий ответ. Одну из причин мы указали - 10 пальцев на руках человека. Возможно, системы с низким основанием (например, пятеричная) оказались менее пригодными, чем десятичная, потому что в них даже сравнительно небольшие числа выражались довольно громоздко. Или, может быть, использование системы с высоким основанием, таких как двадцатеричная или шестидесятеричная, не оправдалось на практике, поскольку требовалось запоминать большое число особых слов - названий низших числительных. Вероятно, поэтому в процессе естественного отбора в подавляющем большинстве случаев выжила система счисления с основанием "средней" величины, т. е. десятичная.

Число 2 - это самое меньшее из чисел, которое можно взять за основание системы счисления. Поэтому в двоичной системе счисления всего две цифры: 0 и 1. С их помощью можно "сосчитать" любые числа. Ведь мы уже убедились в том, что системы счисления с любым основанием равноправны.

Число в двоичной системе запишется так:

M = a n∙2 n+ a n-1∙2 n-1+ ... + a 1∙2 + a 0

Если в десятичной системе "вес" каждой позиции (или разряда) числа равен 10 в некоторой степени, то в двоичной системе вместо числа 10 используется число 2. "Веса" первых 13 позиций (разрядов) двоичного числа имеют следующие значения:

Попробуем записать уже привычное нам число (777) 10в двоичной системе счисления. Мы сможем легко сделать это, вспомнив принцип последовательного деления числа на основание системы, в данном случае числа 777 на число 2:

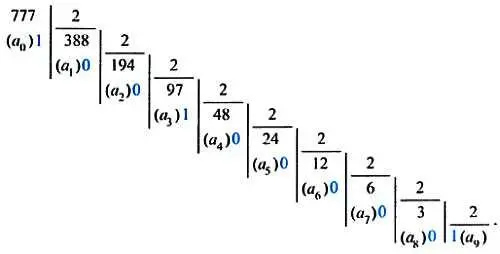
Представляя наше число в виде разложения по степеням двойки и отбрасывая потом при записи сами степени, получаем его запись в двоичной системе:

(777) 10= 1∙2 9 + 1∙2 8 + 0∙2 7 + 0∙2 6 + 0∙2 5 + 0∙2 4 + 1∙2 3 + 0∙2 2 + 0∙2 + 1 = ( 1100001001) 2

Итак, в двоичной системе счисления вместо числа 777 приходится писать число 1100001001.

Другой пример: десятичное число (45) 10имеет двоичную запись (101101) 2.

При записи числа в десятичной системе каждая позиция занята десятичной цифрой. Аналогично при записи числа в двоичной системе каждая позиция занята двоичной цифрой. В научном мире вместо двух слов "двоичная цифра" употребляют одно слово: "бит". Оно произошло от английского bit, составленного из начальных и конечной букв словосочетания binary digit, что в переводе означает "двоичная цифра". Мы можем сказать, что двоичная запись числа (45) 10содержит шесть бит, а числа (777) 10- десять бит.

С помощью одного бита можно записать только числа 0 и 1, двух бит - числа от 0 до 3, трех бит - числа от 0 до 7, четырех бит — числа от 0 до 115 и т.д.

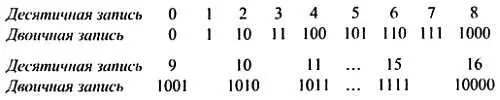
Чтобы записать числа от 0 до 1000, пот ребуется десять бит. В двоичной системе счисления даже сравнительно небольшое число занимает много позиций.