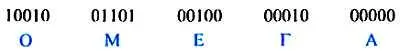Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

Нам неизвестна таблица кодов Бэкона, но мы можем сами, раз принцип известен, придумать какой-либо двоичный код.

Давайте в последней таблице, с помощью которой кодировали фразу "Магические цифры" (см. с. 31), десятичные номера строк и столбцов запишем в двоичной системе счисления:

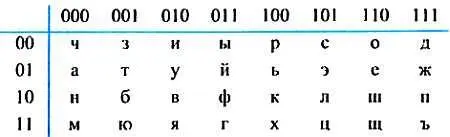
Будем, как и раньше, заменять буквы номерами строк и столбцов, на пересечении которых они стоят, но номерами, представленными двоичными числами. Тогда буквенный текст "Магические цифры" в 5-разрядном двоичном коде примет следующий вид:

Еще раз обращаем ваше внимание на то, что буквы в таблице размещены произвольно, порядок нумерации строк и столбцов также может быть каким угодно. Поэтому можно придумать множество кодов, отображающих буквы выбранного алфавита 5-разрядной комбинацией цифр 0 и 1. Такую комбинацию будем называть, как и в коде Бэкона, двоичным кодовым словом. К примеру, букве "м" соответствует двоичное кодовое слово 11000.

Важно другое. Если двоичное кодовое слово состоит из пяти разрядов (т. е. содержит пять бит), то всевозможных комбинаций цифр 0 и 1 в таком слове будет 2 5= 32. Значит, 5-разрядными двоичными словами можно закодировать алфавит, число букв (или других знаков) которого не превышает 32. Если же исходный алфавит содержит большее число знаков, двоичные слова должны содержать большее число разрядов (бит). Так, словами из шести бит удается заменить 2 6= 64 буквы и знака; словами, содержащими семь бит, — 2 7= 128 букв и знаков; словами из восьми бит — 2 8= 256 букв и знаков и т. д.

В десятом томе "Всеобщей истории" древнегреческого историка Полибия (ок. 201–120 гг. до н. э.) описан способ передачи сообщений на расстояние с помощью факелов (факельный телеграф [1] Слово "телеграф" происходит от греческих слов τηλε (вдаль, далеко) и γραφω (пишу) и означает: передача текста на расстояние. ), изобретенный александрийскими учеными Клеоксеном и Демоклитом. Попробуем, не вникая в суть описанного Полибием изобретения, сами построить факельную систему передачи сообщений.

Имеющиеся в нашем распоряжении световые сигналы не отличаются разнообразием: горящий факел может быть поднят для передачи сообщения вверх или опущен вниз и спрятан за укрытие. Таким образом, налицо всего два состояния — 1, когда горящий факел поднят для передачи сообщения, и 0, когда он опущен. В греческом алфавите 24 буквы. Чтобы представить эти буквы двоичным кодом, потребуется пять разрядов (бит), так как 2 4= 16, а 2 5=32. А это значит, что для технической реализации системы передачи сообщений нам понадобятся пять факелов. Составим кодовую таблицу:

Чтобы яснее различать, когда факелы подняты, а когда убраны, спроектируем стену с зубцами, между которыми имеется пять промежутков (проемов). В промежутки будут вставляться горящие факелы в соответствии с двоичным кодом.

Допустим, нам надо передать слово ОМЕГА (так называется буква Q греческого алфавита). Каждой последовательно "зажигаемой" букве будет соответствовать определенная 5-разрядная двоичная комбинация:

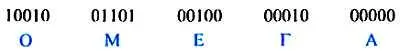
Это означает, что при передаче буквы О горящие факелы должны быть выставлены в первом и четвертом промежутках стены, буквы М — во втором, третьем и пятом промежутках и, наконец, буквы Е — только в третьем, а буквы Г — только в четвергом промежутках. При передаче же буквы А ни один из факелов не должен выставляться.

Для четкой работы факельного телеграфа необходимо придумать специальные сигналы, извещающие о начале и конце передачи (например, помахать факелом).

Теперь обратимся к трудам историка Полибия и посмотрим, как спроектировали факельную систему передачи сообщений Клеоксен и Демоклит. Древнегреческие ученые положили в основу своей системы иной код. Все буквы алфавита они поместили в таблицу 5х5, а номера строк и столбцов закодировали следующими двумя одинаковыми 5-разрядными двоичными кодами:

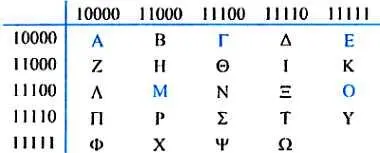
Передача каждой буквы у Клеоксена и Демоклита осуществлялась двумя 5-разрядными двоичными словами. Например, код слова ОМЕГА имел бы в этой системе вид: