Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

⇒ log a(N 1· N 2) = L 1+ L 2= log aN 1+ log aN 2.

Таким образом, логарифм произведения равен сумме логарифмов его множителей.

Если мы сделаем таблицу с двумя величинами, числами и десятичными логарифмами, то сможем сложить логарифмы и при помощи таблиц легко узнать произведение. И хотя сегодня можно без труда произвести умножение электронными калькуляторами, во времена, когда они еще не существовали, операция, помогающая заменить сложные расчеты в случаях произведений больших величин на простое сложение, имела огромное практическое значение.

Проследим за хитроумными рассуждениями Эйлера, но не будем забывать, что в некоторых местах они должны быть доработаны. Позже это сделал сам ученый. Возьмем знаменитый ряд Тейлора:

sinx = x - x 3/3! + x 5/5! - x 7/7! + ...

Мы знаем, что он равен нулю при х равном нулю, то есть если sinx = 0, когда х = 0, ± π, ±2π, ±3π...

Следовательно, предположив, что ряд ведет себя как многочлен, поскольку он и является длиннейшим многочленом, применение фундаментальной теоремы алгебры преобразит его в произведение одночленов вида х - α, где α — решение. Продолжим:

x - x 3/3! + x 5/5! - x 7/7! + ... = K(x)(x - π)(x + π)(x - 2π)(x + 2π)...

К — неизвестная константа. Производя вычисления в правой части равенства:

x - x 3/3! + x 5/5! - x 7/7! + ... = K(x)(x 2- π 2)(x 2- 4π 2)(x - 9π 2)...

следует отметить, что каждый член вида х 2- λ 2π 2справа равен нулю. А это происходит, только если

1 - х 2/(λ 2π 2) = 0.

Запишем члены правого выражения в следующей форме:

x - x 3/3! + x 5/5! - x 7/7! + ... = K(x)(1 - x 2/π 2)(1 - x 2/4π 2)(1 - x 2/9π 2)...

Теперь разделим на x:

sinx/x = 1 - x 2/3! + x 4/5! - x 6/7! + ... = K(1 - x 2/π 2)(1 - x 2/4π 2)(1 - x 2/9π 2)...

И, поскольку lim x→0(sinx/x) = 1, получим, что K = 1. Итак:

1 - x 2/3! + x 4/5! - x 6/7! + ... = (1 - x 2/π 2)(1 - x 2/4π 2)(1 - x 2/9π 2)...

Этот ряд равен бесконечному произведению. Для Эйлера это не проблема. Подсчитаем порядок произведения и выделим члены произведения с x 2в правой части:

- x 2/3! = -x 2/π 2- x 2/4π 2- x 2/9π 2- ...

Разделив обе части на -x 2/π 2, получим

π 2/6 = 1+ 1/2 2+ 1/2 3+ 1/4 2+ ...,

что и требовалось доказать.

Эйлер был первым математиком, доказавшим тождественность ζ($) как ряда степеней и ζ($) как бесконечного произведения. Назовем р кпростое число, занимающее место k в ряде. Получим

Ниже можно увидеть, каким образом получается это равенство:

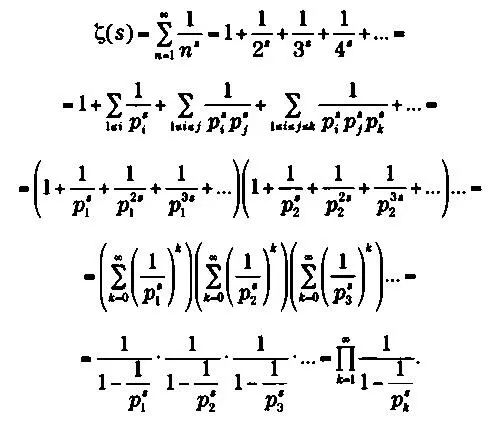
Для тех, кто знаком со сложным анализом, дзета-функция может быть расширена до мероморфной во всей комплексной области с простым полюсом s = 1, где остаток равен 1. Это дзета-функция, о которой говорил Риман и которая стала предметом его знаменитой гипотезы.

Чтобы упростить, насколько это возможно, наше объяснение, оттолкнемся от предположения, что задействованные в нем функции удовлетворяют всем необходимым условиям на производную и непрерывность.

Обозначим через S функционал (функцию функций), к которому мы применим вариационное исчисление, а через x 1,х 2— экстремумы неизвестной функции:

S(ƒ) = ∫ x1 x2L(x 1,ƒ(x),ƒ'(x))dx.

Предположим, что решением является ƒ 0и что функционал имеет здесь минимум; назовем α(x) функцию (которую мы будем "варьировать"), равную нулю в экстремумах x1, х 2. Поскольку в ƒ 0функционал имеет минимум,

S(ƒ 0)≤S(ƒ 0+εα)

в окрестности ƒ 0. Вариационный размах

ƒ = ƒ 0+ εα

должен удовлетворять:

dS(ƒ 0+ εα)/dε|ε=0 = ∫ x1 x2dL/dε| ε=0= 0

Теперь вспомним, что

dƒ/dε = α,dƒ'/dε = α'.

Применим правило дифференцирования и проведем необходимые замены.

Получим

dL/dε = ∂L/∂ƒ dƒ/dε + ∂L/∂ƒ' dƒ'/dε = (∂L/∂ƒ)α + ∂L/∂ƒ'α'

A теперь проинтегрируем по частям и учтем предыдущую формулу:

Поскольку выражение слева — ноль, то нулем будет и выражение справа. Следовательно,

dL/dƒ = d/dx ∂L/dƒ' = 0

Таким образом, мы получили уравнения Эйлера — Лагранжа, которые в приложениях обычно приводят к дифференциальным уравнениям второго порядка.

5. КОМПЛЕКСНЫЕ ЧИСЛА

Эйлер вывел свою фундаментальную формулу, из которой впоследствии получил еще несколько из простых рядов Тейлора. Напомним, что степени ведут себя так:

i0 = 1,i1 = i,i2 = -1,i3 = -i,

i 4- 1, i 5= i, i 6= 1,i7 = i и так далее.

Напомним также, что ряды степеней е и тригонометрических функций синус и косинус раскладываются в ряд Тейлора или степенной ряд следующим образом: