7 = 7
7 = 6 + 1
7 = 5 + 2
7 = 5+ 1 + 1
7 = 4 + 3
7 = 4 + 2 + 1
7 = 4 + 1 + 1 + 1
7 = 3+3+1
7 = 3 + 2 + 2
7 = 3 + 2 + 1 + 1
7 = 3 + 1 + 1 + 1 + 1
7 = 2 + 2 + 2 + 1
7 = 2 + 2 + 1 + 1 + 1
7 = 2 + 1 + 1 + 1 + 1 + 1
7 = 1 + 1 + 1 + 1 + 1 + 1 + 1.
Итого 15. Запишем: р(7) - 15. Этот простой пример показывает, что разложить число — трудная задача, а результат может быть непредсказуемым. Если мы подсчитаем первые значения р(х), то получим:
Р(1) = 1
Р(2) = 2
P(3) = 3
Р(4) = 5
Р(5) = 7
P(6) = 11
Р(7) = 15
Р(8) = 22
P(9) = 30
P(10) = 42.
Никаких странностей не наблюдается, мы видим только, что p возрастает. Можно доказать, что
р(100) = 190569292.
СРИНИВАСА РАМАНУДЖАН АЙЕНГОР
Этот индийский математик родом из далекой страны, с непростой судьбой и необыкновенным талантом, привнес нотку экзотики в научный мир своего времени. Он родился в Эроде, в штате Тамил-Наду, и был типичным представителем своего общества, очень религиозным и строго соблюдавшим вегетарианство. Рамануджан был гением-самоучкой. По совету друзей он отправил несколько писем в Лондон, в которых рассказывал о своих результатах. Одно из них попало в руки к Годфри Харолду Харди (1877-1947). Вместе со своим другом и коллегой Джоном Литлвудом (1885- 1977) Харди проанализировал содержание писем, в которых говорилось обо всем сразу: об открытиях, уже сделанных, в том числе и самим Харди, и о новых формулах, свидетельствовавших о необыкновенных математических способностях. По приглашению Харди Рамануджан приехал в Англию и впоследствии был избран членом кембриджского Тринити-колледжа и Королевского общества. Многие его разработки еще не до конца изучены, но все единодушно отмечают их красоту, глубину, изобретательность и новизну. Рамануджан углубил работы Эйлера по разбиению, и это принесло свои плоды: многое из того, что сегодня об этом известно. — плод его исследований. Благодаря гению Рамануджана, мы располагаем "простым" инструментом, с помощью которого можем узнать примерное количество разбиений любого числа:
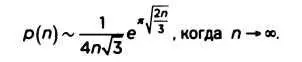
Его можно получить с помощью калькулятора. При желании мы можем получить точные цифры, а не приблизительные, но процесс будет немного сложнее.

Ученые получили необыкновенно длинные результаты, выявили малейшие различия между разбиением четных и нечетных чисел (состоящих только из четных или нечетных чисел), изобрели сложнейшие арифметические инструменты. Большая часть удивительных работ Эйлера основана на методах, развитых Абрахамом де Муавром, которые заключаются в игре со степенными рядами. Так он получал то, что в то время называлось производящими функциями последовательности, то есть хитроумные алгебраические трюки, с помощью которых ученые пытались сымитировать реальность. Уже в 1742 году Эйлеру пришла в голову идея найти производящую функцию разбиений, и после долгих лет работы он пришел к ней: оттолкнувшись от ряда
1/(1 - х) = 1 + х + х 2+ х 3+ ...,
он вывел формулу
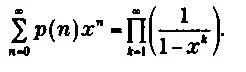
Развивая бесконечное произведение справа, можно доказать, что различные разбиения числа n появляются в скрытой форме в группах степеней меньших n, которые в сумме дают n. Например, возьмем n = 4 и посмотрим, сколько х4 мы получим:
(1 + х + х 2+ x 3+ ...) (1 + х 2+ х 4+ х 6+...)(1 + х 3+ x 6+ х 9+...)...
В результате мы получим 5х4. и следовательно, р(4) = 5. Отсюда Эйлер вывел метод для вычисления р(n), но, к сожалению, это рекурсивный метод, который позволяет вычислить р(n), только если мы знаем предшествующие значения:
р(n) = р(n - 1) +р(n - 2) - р(n - 5) - р(n - 7) + р(n - 12) + р(n - 15) - р(n - 22) - ...
ЧИСЛА БЕРНУЛЛИ
Эти числа были названы в честь Якоба Бернулли, который впервые рассмотрел их в 1713 году в своем сочинении Ars conjectandi ("Искусство предположений"). Эти числа встречаются при вычислении сумм степеней целых положительных чисел:
1 + 2 2+ З 2+ 4 2+ ... + k 2
1 + 2 3+ З 3+ 4 3+ ... + k 3
1 + 2 4+ З 4+ 4 4+ ... + k 4
1 + 2 5+ З 5+ 4 5+ ... + k 5,
или, говоря языком Эйлера, вычислении сумм
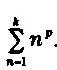
Мы имеем
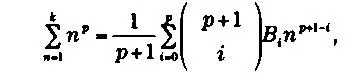
где В i— числа Бернулли. Чтобы пояснить предыдущую формулу, приведем простой пример — сумму квадратов простых чисел. Применив формулу при р - 2, получим
Читать дальше

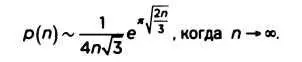

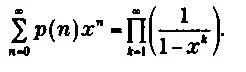
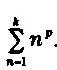
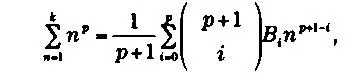





![Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-thumb.webp)



