Joaquin Sandalinas - До предела чисел. Эйлер. Математический анализ.

1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ... ,

который итальянский математик Пьетро Менголи сгруппировал так:

1 + 1/2 + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) +

+ (1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16) + ...

≥ 1 + 1/2 + 1/2 + 1/2 + 1/2 + ... ,

показав, что его сумма бесконечна. Другие же вызывали недоумение. Рассмотрим пример:

1 - 1 + 1 - 1 + 1 - 1 + ...

В таком виде кажется, что его сумма равна 0:

(1-1) + (1-1) + (1-1) + ... = 0,

а если сгруппировать его так, то сумма равна 1:

1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + ... = 1.

На самом деле оба результата неправильны. Эйлер, как и другие математики того времени, предпочитал исходить из известного ряда

1/(1-x) = 1 + x + x 2+ x 3+ x 4+ x 5+ ...

Подставив вместо х число -1, он пришел к

1/2 = 1/(1- (-1)) = 1 + (-1) + (-1) 2+ (-1) 3+ (-1) 4+ (-1) 5+ ...

= 1 - 1 + 1 - 1 + 1 - 1.

то есть ни 1, ни 0: Эйлер утверждал, что сумма равна 1/2.

К арсеналу уже известных к тому времени рядов

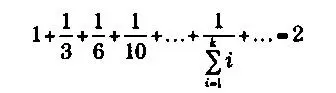
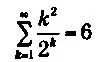
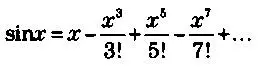
Эйлер постепенно добавил много собственных результатов: решение Базельской задачи; формулу суммирования Эйлера — Маклорена, которая улучшала сходимость, если таковая наблюдалась; преобразование рядов через конечные и последовательные разности; а также важные открытия в области расходящихся рядов. Фактически, в 1755 году, то есть в эпоху, когда еще не существовало понятие предела, ученый уже различал сходящиеся и расходящиеся ряды. Среди рядов, суммированных Эйлером, мы находим

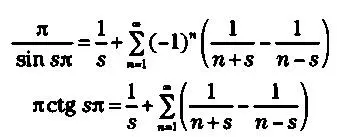
π/(3√3) = 1 - 1/2 + 1/4 - 1/5 + 1/7 - 1/8 + ...

π/(2√2) = 1 + 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + ...

π/3 = 1 + 1/5 - 1/7 - 1/11 + 1/13 - 1/17 + ...

π 2/(8√2) = 1 - 1/3 2- 1/5 2+ 1/7 2+ 1/92 + ...

π 2/(6√3) = 1 - 1/5 2- 1/7 2+ 1/112 + 1/13 2+ ...

1 -1! + 2! -3! + ... = 0,596347362123...

Он также открыл два новых ряда. Один — данная последовательность степеней:

arxtgz = z - z3/3 + z5/5 + z7/7 + ... ,

а вторым был первый ряд Фурье в истории, который Эйлер описал в 1744 году в письме Гольдбаху, то есть задолго до того, как Жозеф Фурье (1768-1830) начал свои знаменитые исследования. И даже до того, как Фурье родился.

1/2x = sinx - 1/2 sin 2х + 1/3 sin Зx - ...

Вклад Эйлера в теорию чисел огромен, и его подробное изложение не является целью этой книги. Достаточно сказать, что только Карл Густав Якоб Якоби (1804-1851) и Сриниваса Рамануджан Айенгор (1887-1920) могут сравниться с ним по значению своих работ в этой области. Еще одним важным разделом математики, интересовавшим Эйлера, были дифференциальные уравнения. Здесь его самым знаменитым открытием, возможно, является метод Эйлера, позволяющий приближенно решать дифференциальные уравнения первого порядка.

Эйлер, имевший серьезные проблемы со зрением, в России мог бы удалиться от дел и спокойно почивать на лаврах. Но он работал до самой смерти: глубоко исследовал теорию чисел, добился превосходных результатов в области простых чисел, чисел Мерсенна и чисел Бернулли, а также диофантовых уравнений и разбиения множеств. Он также успел уделить время игровой математике и даже написал несколько научно-популярных книг.

Причиной возвращения Эйлера в Россию в 1766 году стало желание императрицы Екатерины II вернуть Академии былую славу. Ученый никогда не терял связи с Россией, даже живя в Берлине. Хорошо известно, что он посылал в Санкт- Петербург множество статей, которые были логическим продолжением работ, впервые опубликованных именно в России. Ученый также постоянно получал вознаграждение от Российской империи за решение определенных задач, например военного характера, и оказывал протекцию молодым русским, приезжавшим учиться в Европу. За научный вклад в работу Петербургской академии Эйлеру в 1742 году, когда он еще был в Берлине, была назначена пенсия. Один любопытный исторический факт дает представление не только о подробностях второго путешествия Эйлера в Россию, но и о том, насколько не сложились его отношения с предыдущим покровителем. В одном из своих писем Фридрих сожалел об утере целого ряда личных записок ученого во время кораблекрушения, произошедшего по пути в Санкт-Петербург: "Какая жалость, ведь из этих записок могло бы получиться шесть томов трактатов, полных цифр от начала и до конца, а теперь, видимо, Европа лишилась такого приятного чтения".

По приезду ученого ему было назначено весьма щедрое жалованье в 3000 рублей. Императрица даже отдала ему повара из своего дворца. Руководила Академией, по назначению Екатерины, княгиня Дашкова. Существует знаменитый и документально подтвержденный анекдот, который показывает, как высоко княгиня ценила Эйлера. Однажды она провожала ученого в зал собраний. Один напыщенный профессор захотел сесть на почетное место рядом с председательницей, она же насколько можно любезно обратилась к Эйлеру: "Располагайтесь, где хотите, господин Эйлер, хотя все мы знаем, что вы выберете самое почетное место, первое из всех".