Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

Георг Кантор, около 1880 года.

Первая страница статьи «Об одном свойстве совокупности всех действительных алгебраических чисел», опубликованной Кантором в 1874 году. В ней уже содержались некоторые из основных идей будущей теории бесконечности.

Карл Вильгельм Борхардт, издатель <���Журнала Крелле· с 1856 по 1880 год.

Немецкий математик Леопольд Кронекер. Он был убежден в том, что вся теорема существования должна основываться на реальном построении и развиваться в конечное число этапов, а потому отверг теорию множеств, предложенную Кантором, и положил начало обширному спору.

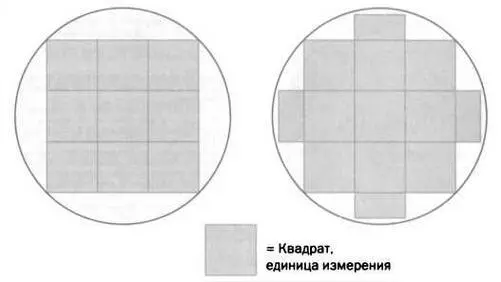
РИС. 6

Теория [бесконечных множеств] — это область, в которой нет ничего очевидного, ее истинные положения часто звучат парадоксально, а кажущиеся истинными на самом деле являются ложными.

Немецкий математик Феликс Хаусдорф, 1914 год

РИС. 7

Основываясь на этой идее и исходя из свойств правильных многоугольников, уже известных в то время, Евдокс доказал, что площадь любой окружности пропорциональна площади квадрата, построенного на ее радиусе. Это означает, что если радиус окружности равен r, то его площадь высчитывается при умножении r 2на число, одинаковое для всех окружностей. В XVIII веке великий швейцарский математик Леонард Эйлер (1707-1783) обозначил это число греческой буквой π, и сегодня мы говорим, что площадь окружности равна π ∙ r 2.

Через 100 лет после Евдокса Архимед использовал похожий подход для того, чтобы рассчитать объем сферы, а также площадь и центр тяжести различных фигур, ограниченных кривыми. Ему также удалось получить наиболее точное значение числа π в истории Античности.

Тем не менее методы древнегреческих ученых были недостаточно обобщенными: для каждого вычисления требовалось отдельное построение, которое работало только для конкретного случая. Так, например, способ Евдокса вычислить площадь окружности не мог быть применен к эллипсу, все рассуждения грека относились только к окружности и ни к какой другой фигуре.

Правильный многоугольник с 4 сторонами

Правильный многоугольник с 7 сторонами

Правильный многоугольник с 11 сторонами

РИС. 8

С XVI века европейские математики принялись искать общий способ решения вопроса о площади фигур, ограниченных кривыми. Самых выдающихся результатов добились четверо математиков: Иоганн Кеплер (1571-1630), Бонавентура Кавальєри (1598-1647), Рене Декарт (1596-1650) и Пьер де Ферма (1601-1665). В конце XVII века Исаак Ньютон (1643-1727) и Готфрид Лейбниц (1646-1716), опираясь на достижения своих предшественников, независимо друг от друга нашли наконец общий метод расчета площади любой плоской фигуры. Это один из основных инструментов исчисления, и называется он интегральным.

Юлиус Вильгельм Рихард Дедекинд родился 6 октября 1831 года в Брауншвейге, Германия. С детства он проявлял огромный интерес к наукам и постепенно сконцентрировался именно на математике. В 1848 году поступил в Карловский коллегиум, где преподавание соответствовало университетскому уровню, поэтому Дедекинд получил солидное образование в области алгебры, аналитической геометрии и исчисления. Он дополнил его в Геттингенском университете, куда поступил в 1850 году. Два года спустя он получил там степень доктора под руководством самого Карла Фридриха Гаусса, одного из величайших математиков в истории.